Fit a Gaussian process to spatial proteomics data
Source:R/fitGP.R, R/fitGPmaternPC.R
bandle-gpfit.RdThe fitGP function is a helper function to fit GPs with squared
exponential co-variances, maximum marginal likelihood
The fitGPmaternPC function is a helper function to fit matern GPs to
data with penalised complexity priors on the hyperparameters.
The fitGPmatern function fits matern GPs to data.
The plotGPmatern function plots matern GPs
Arguments
- object
A instance of class
MSnSet- fcol
feature column to indicate markers. Default is
"markers".- materncov
logicalindicating whether matern covariance is used.- nu
matern smoothness parameter. Default is 2.
- hyppar
The vector of penalised complexity hyperparameters, you must provide a matrix with 3 columns and 1 row. The order is hyperparameters on length-scale, amplitude, variance.
- params
The output of running
fitGPmatern,fitGPmaternPCorfitGPwhich is of classgpParams
Value
Returns an object of class gpParams which stores the posterior
predictive means, standard deviations, variances and also the MAP
hyperparamters for the GP.
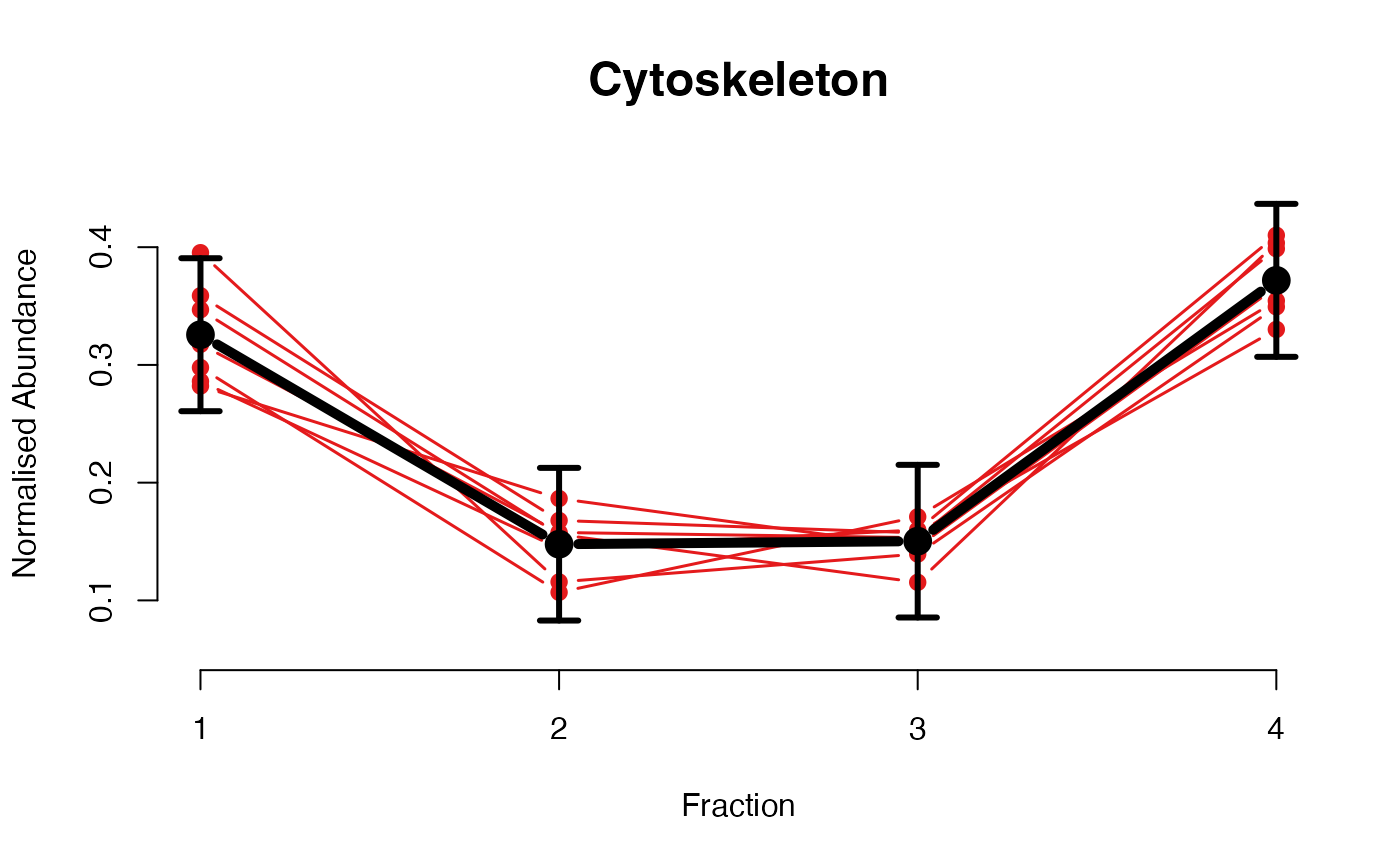
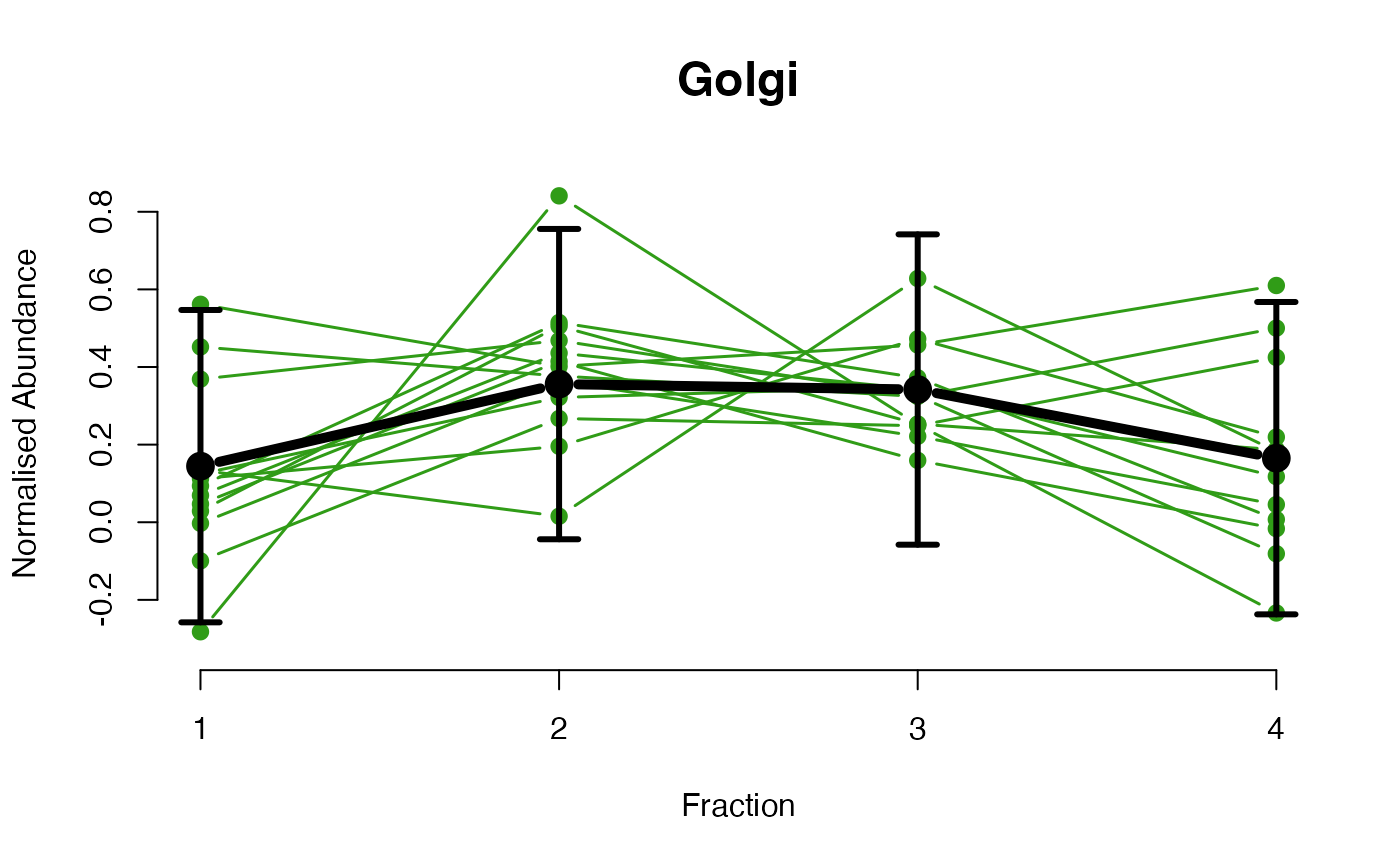
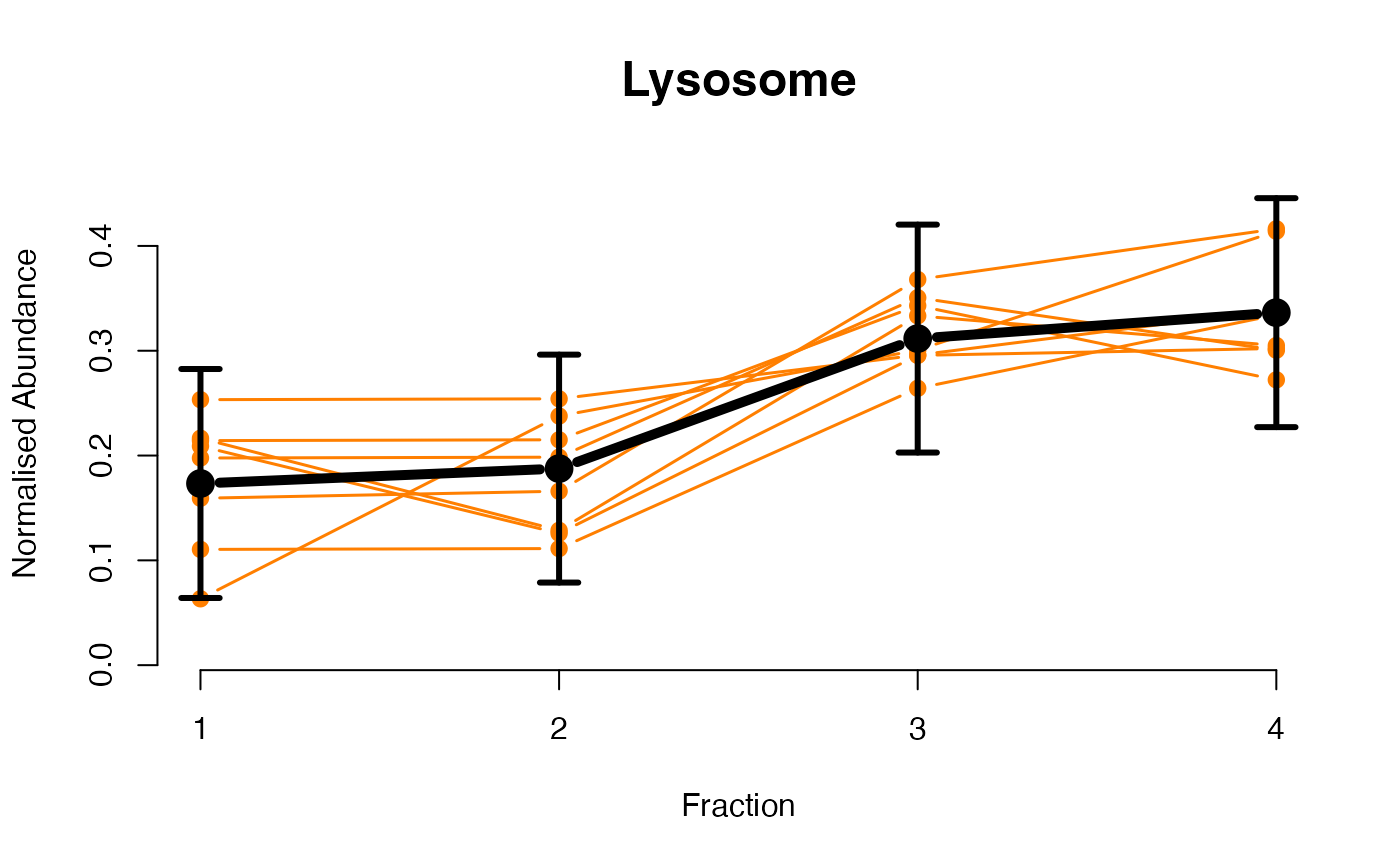
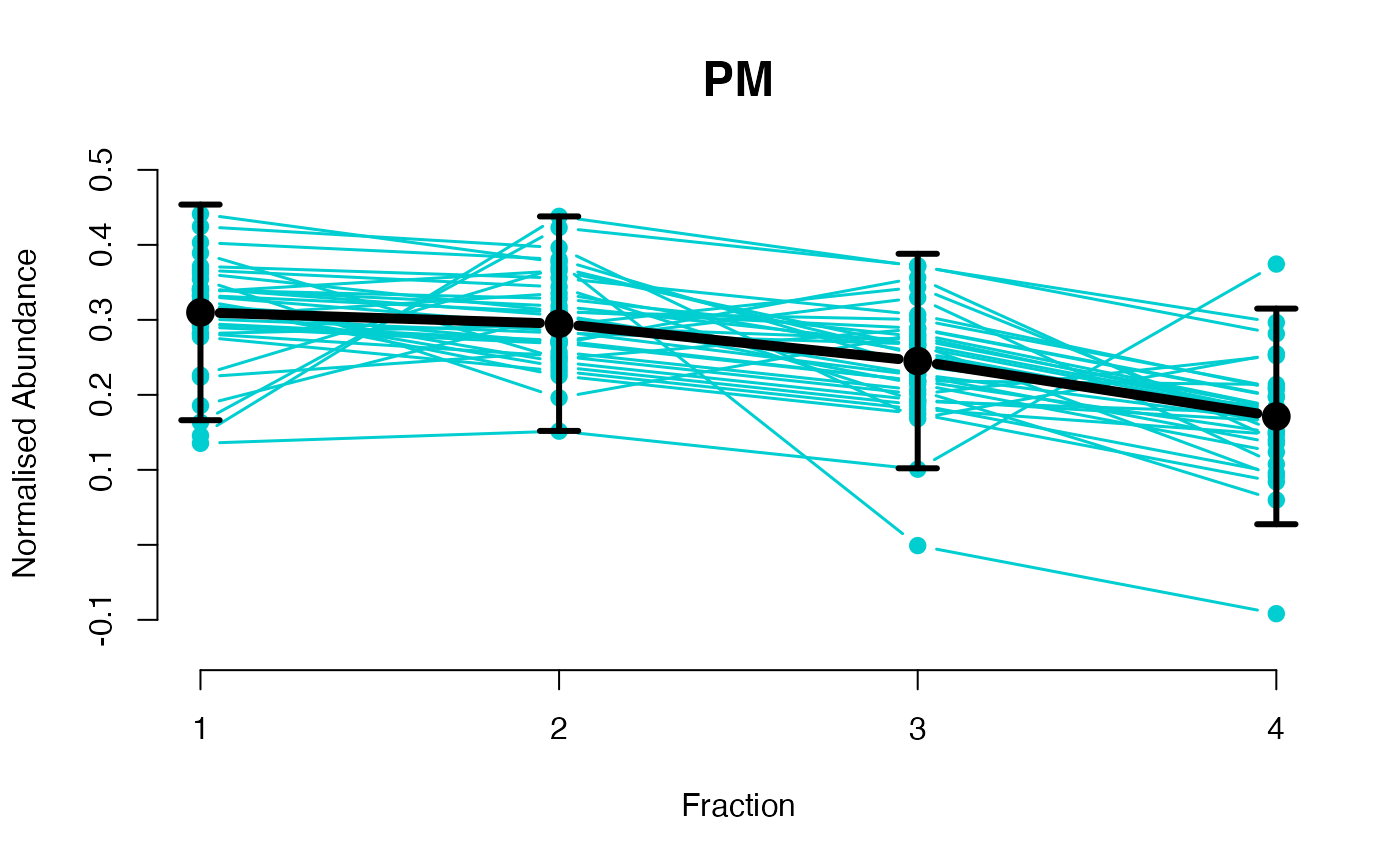
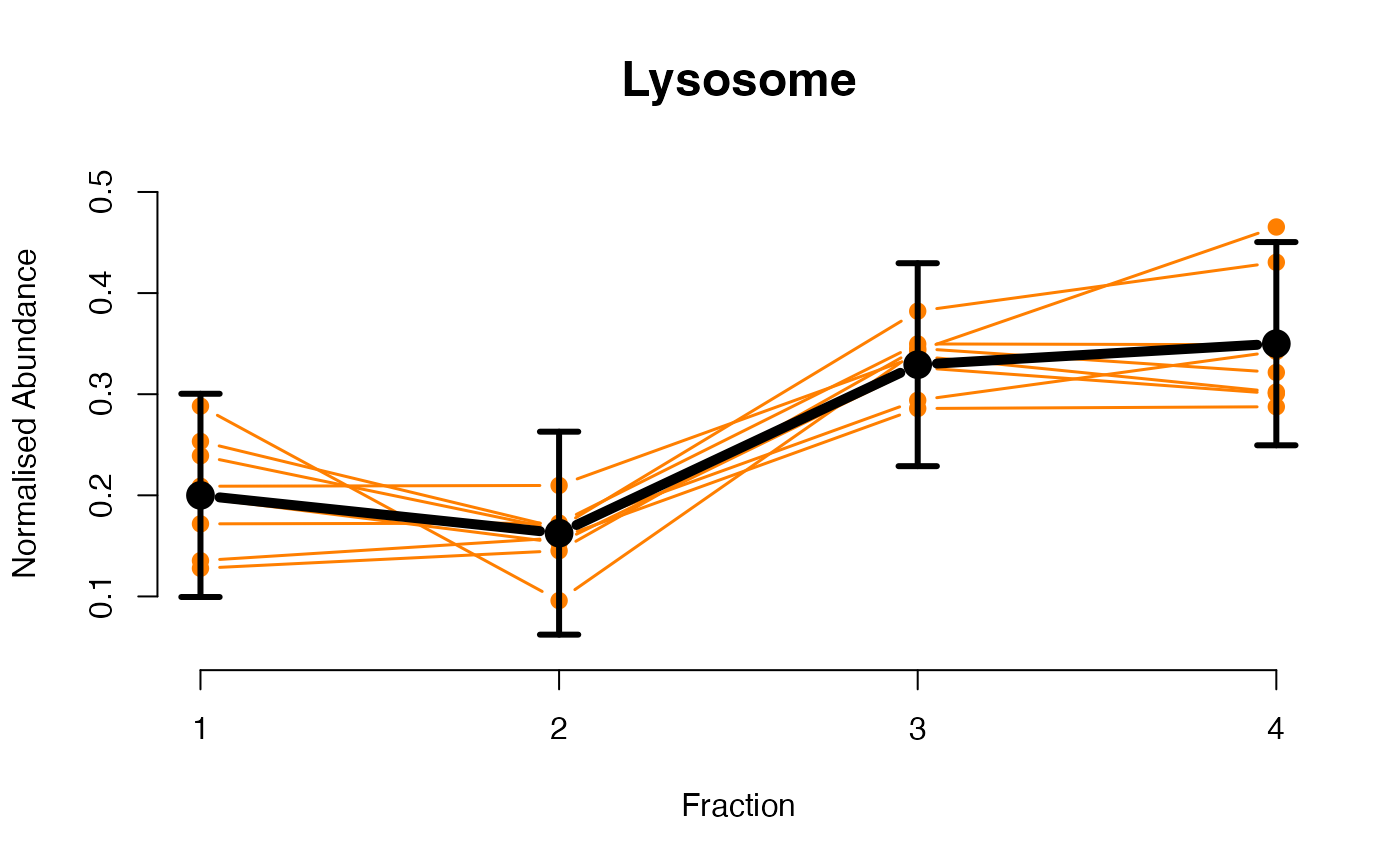
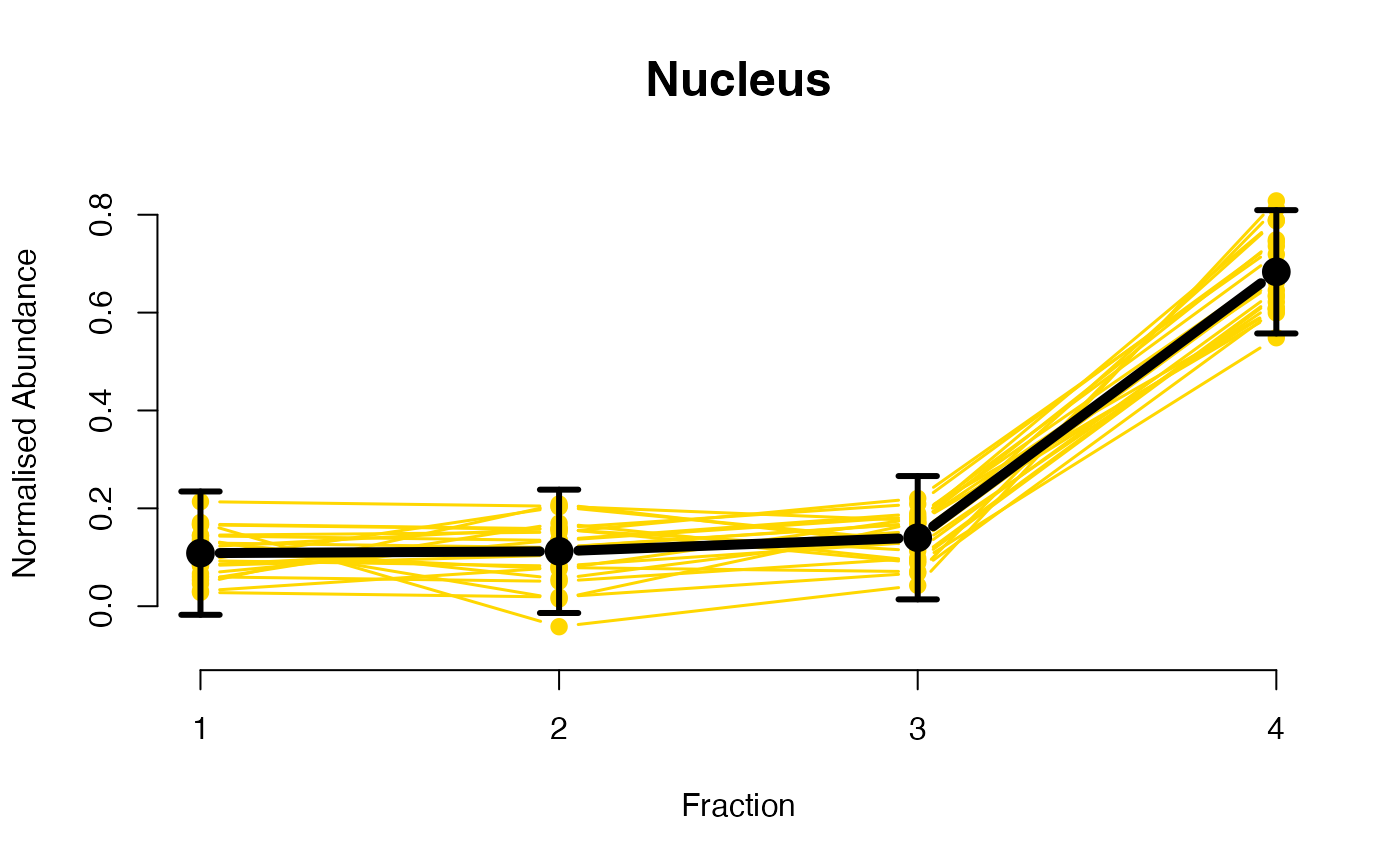
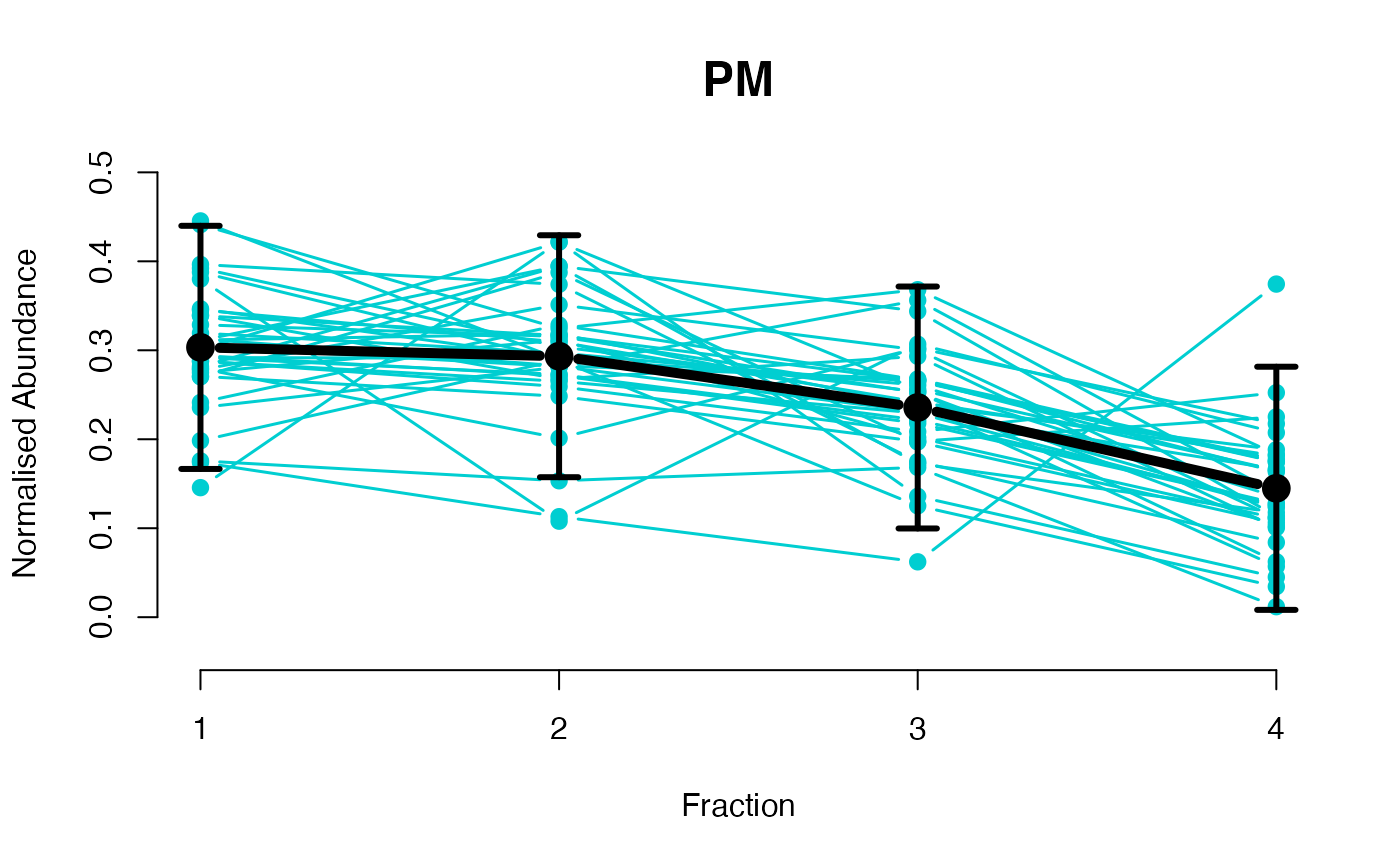
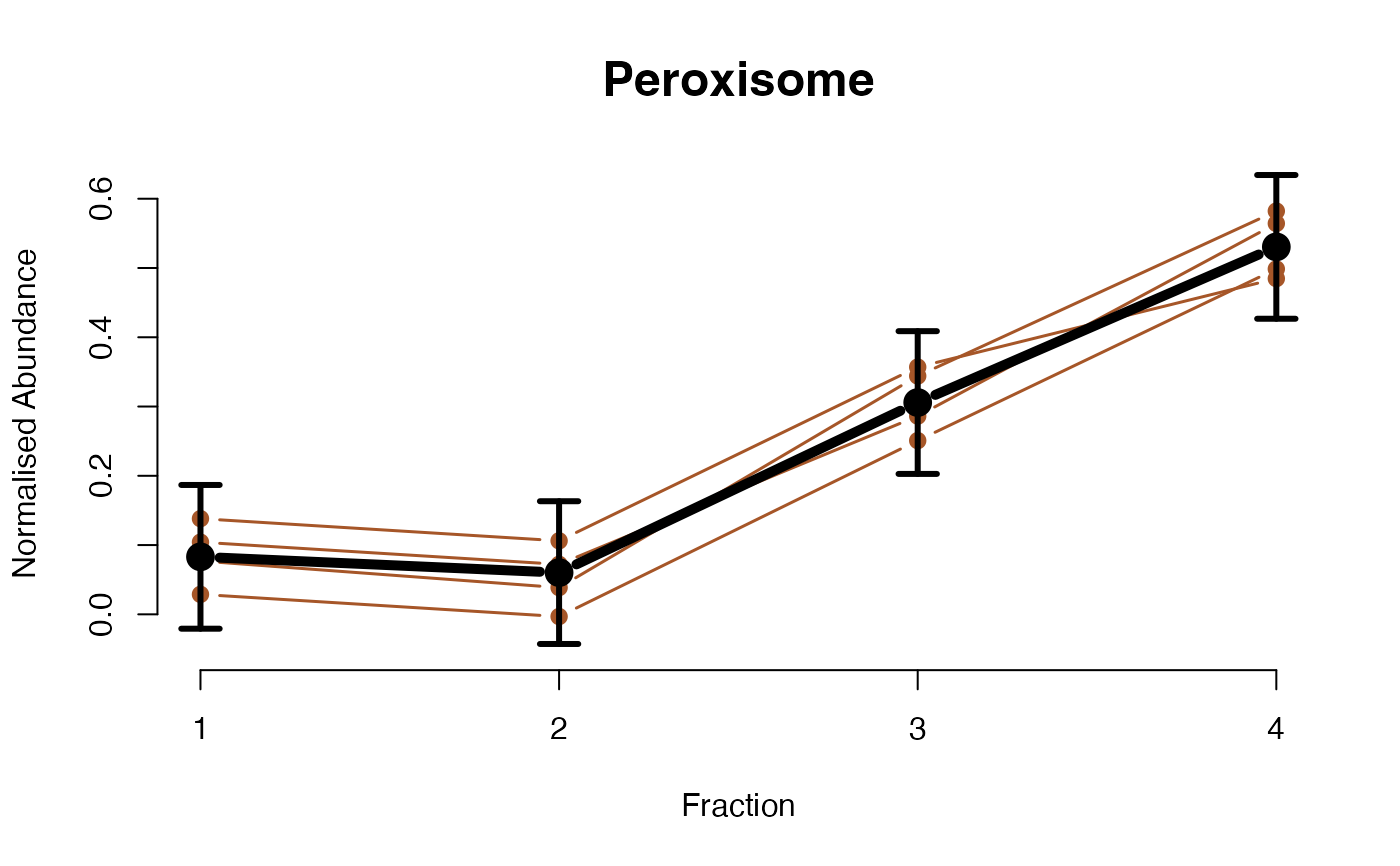
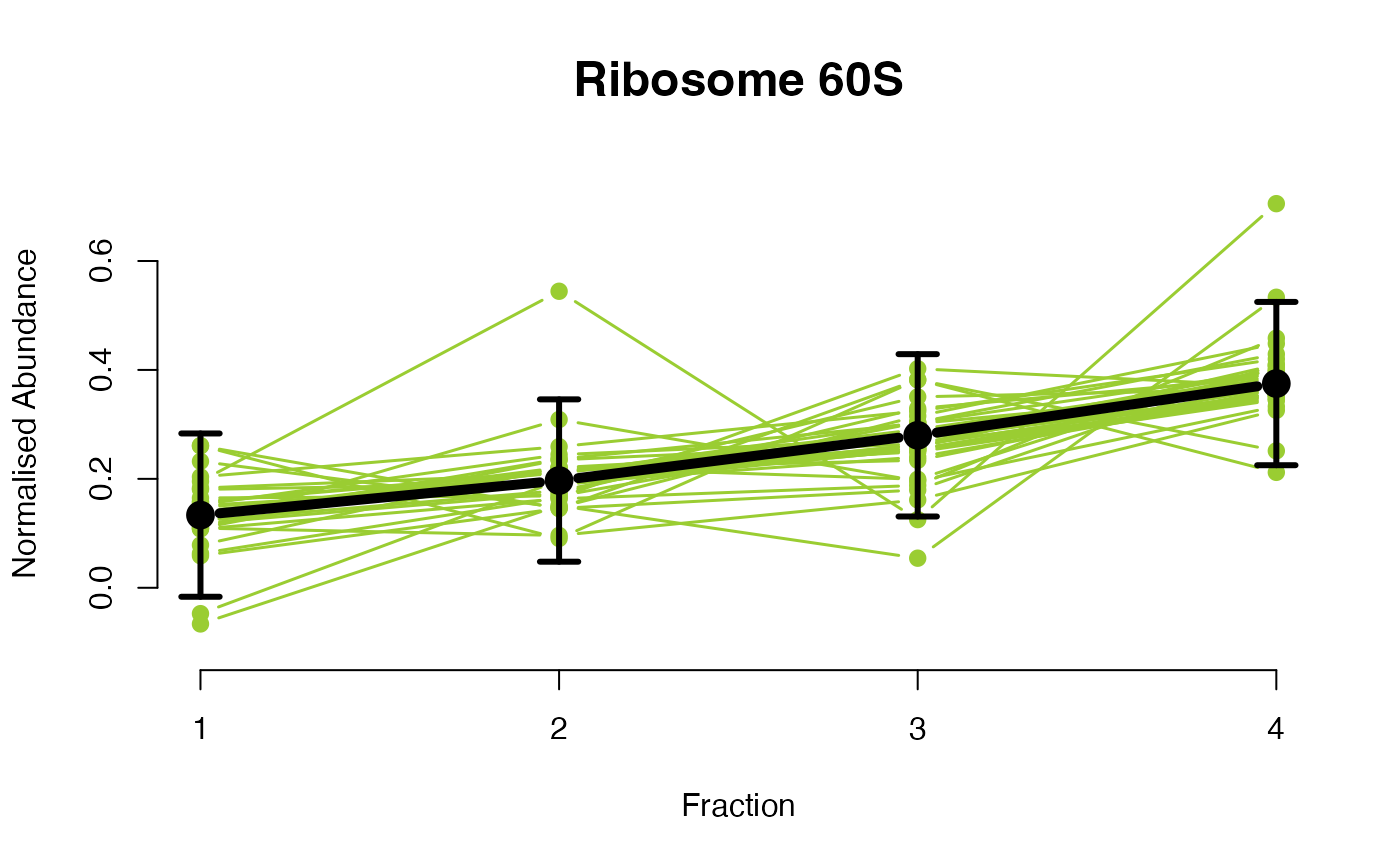
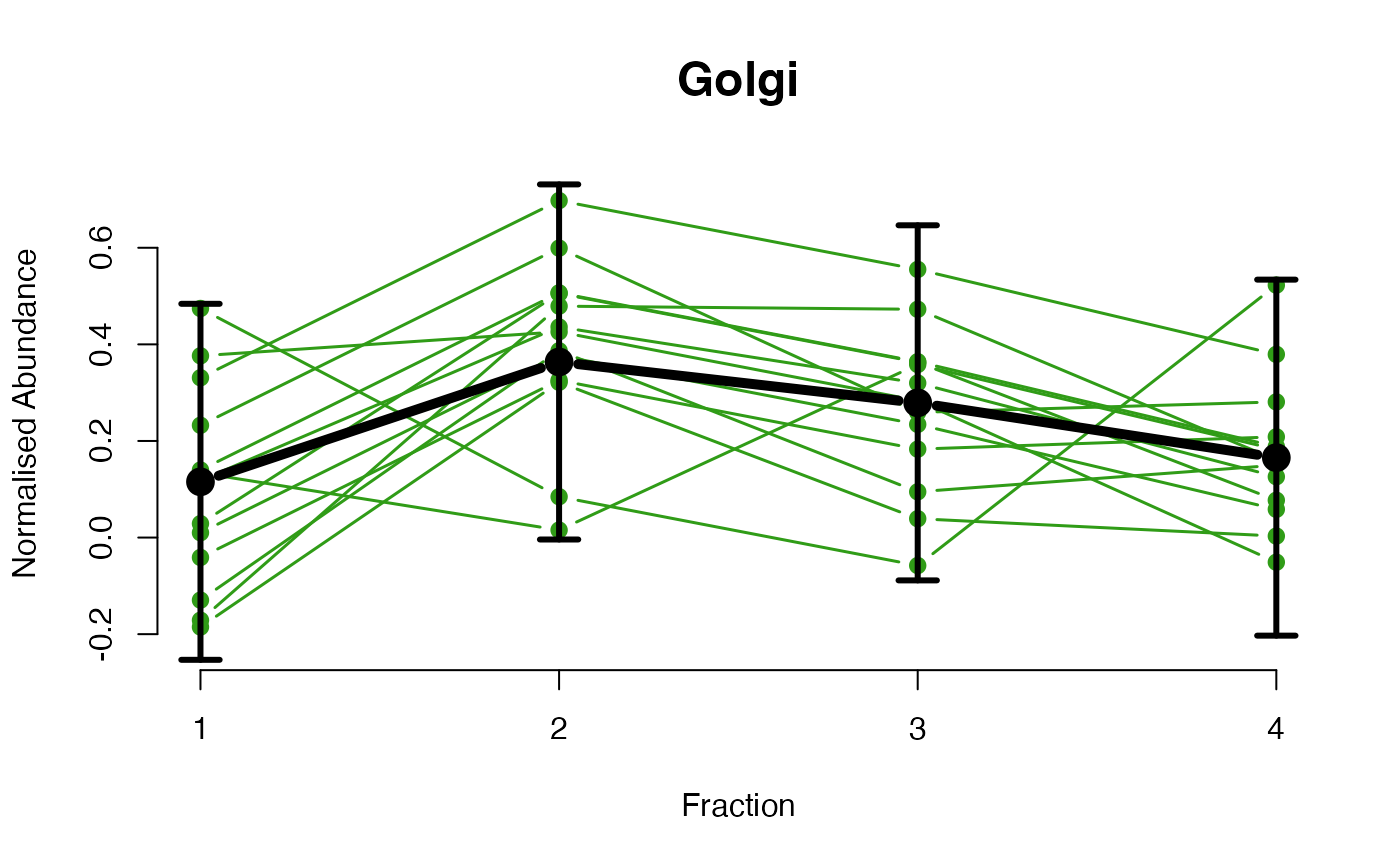
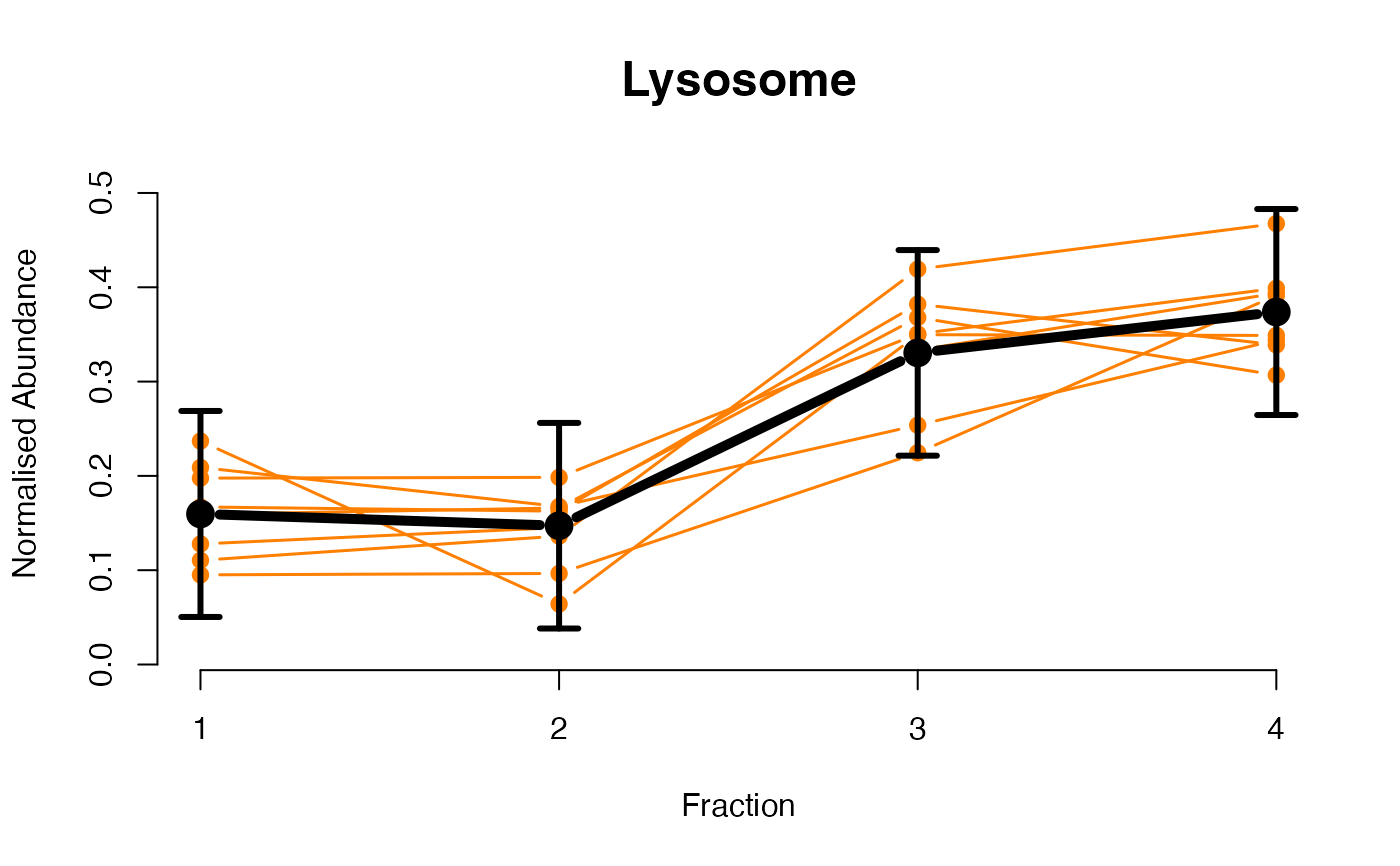
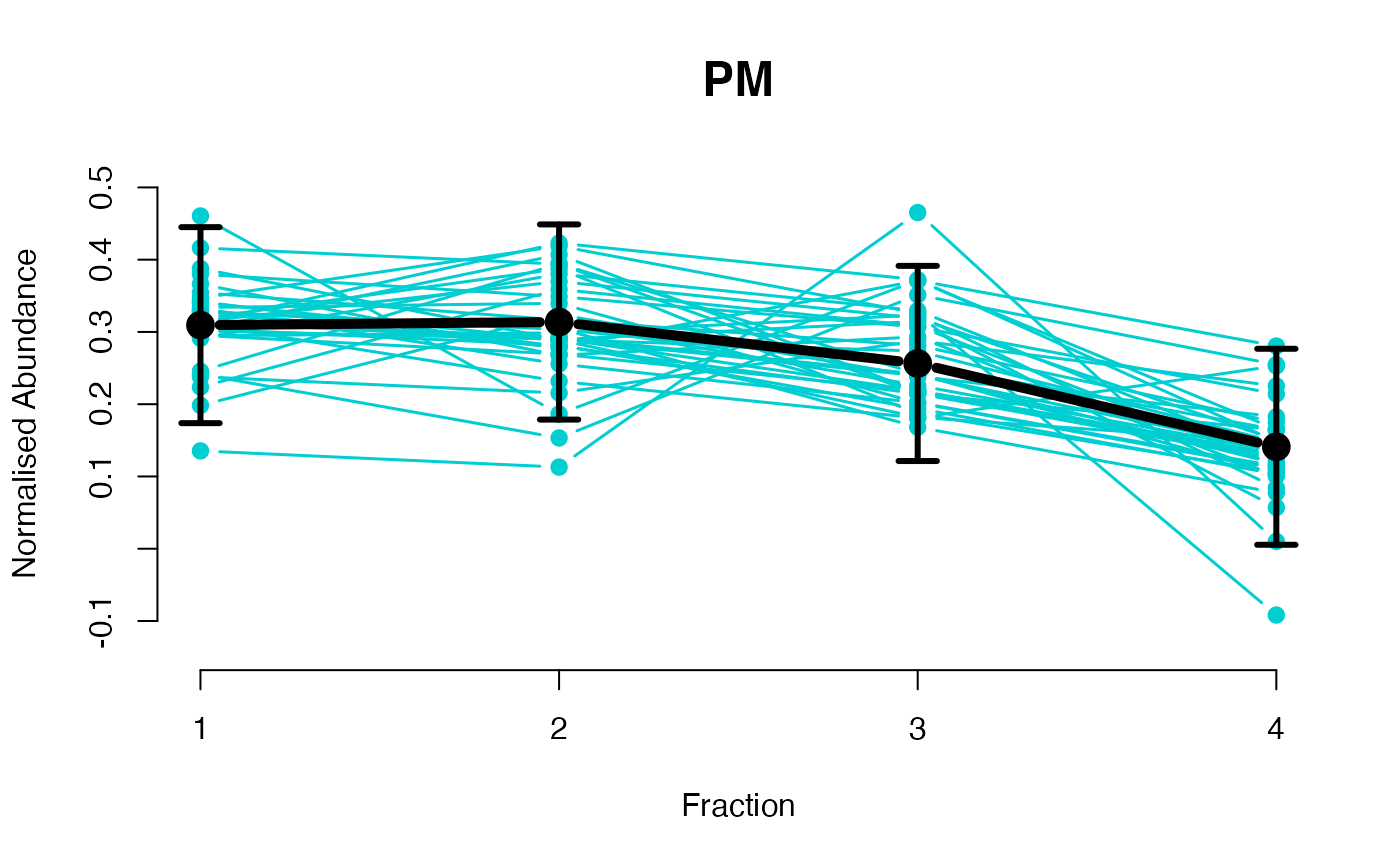
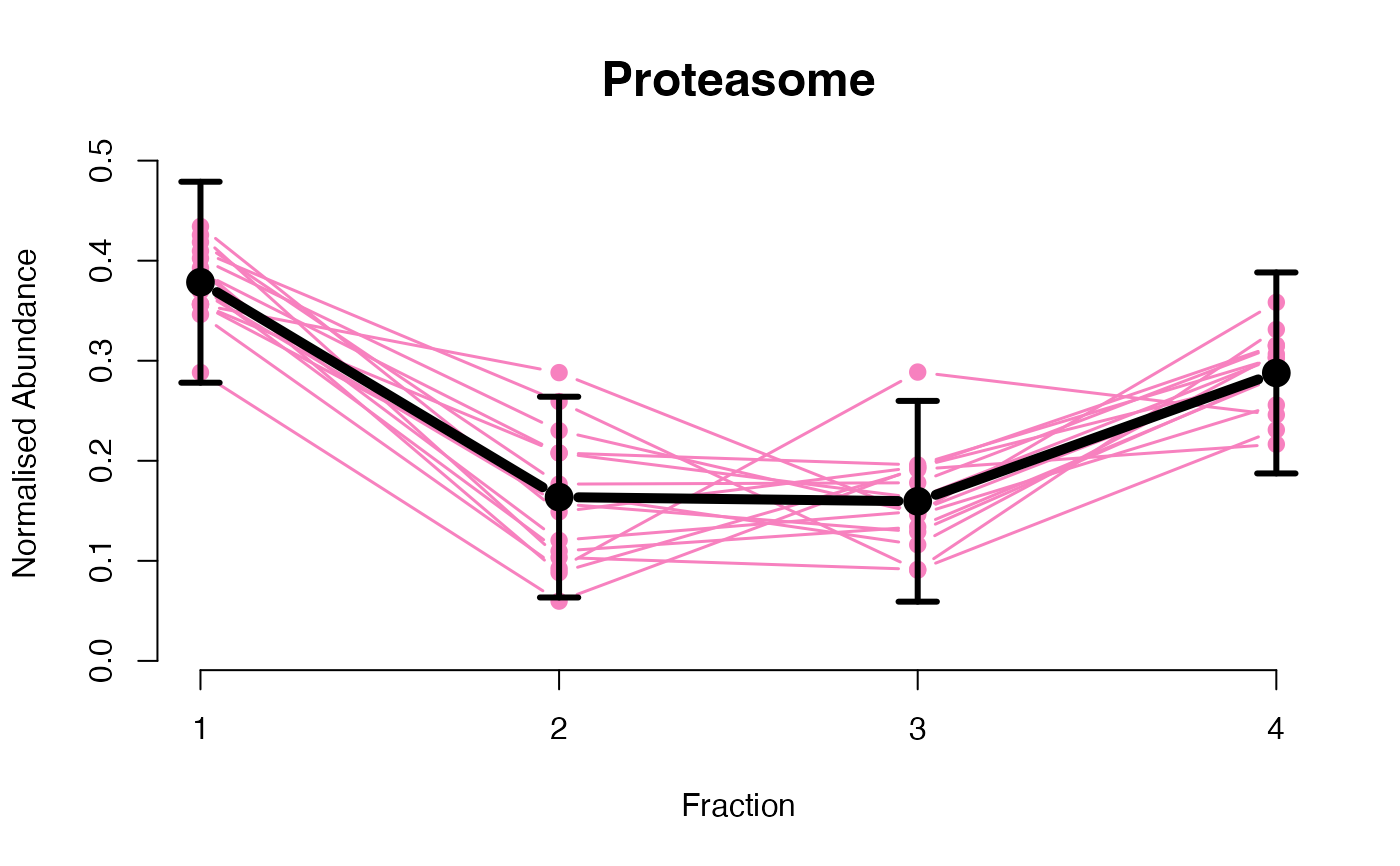
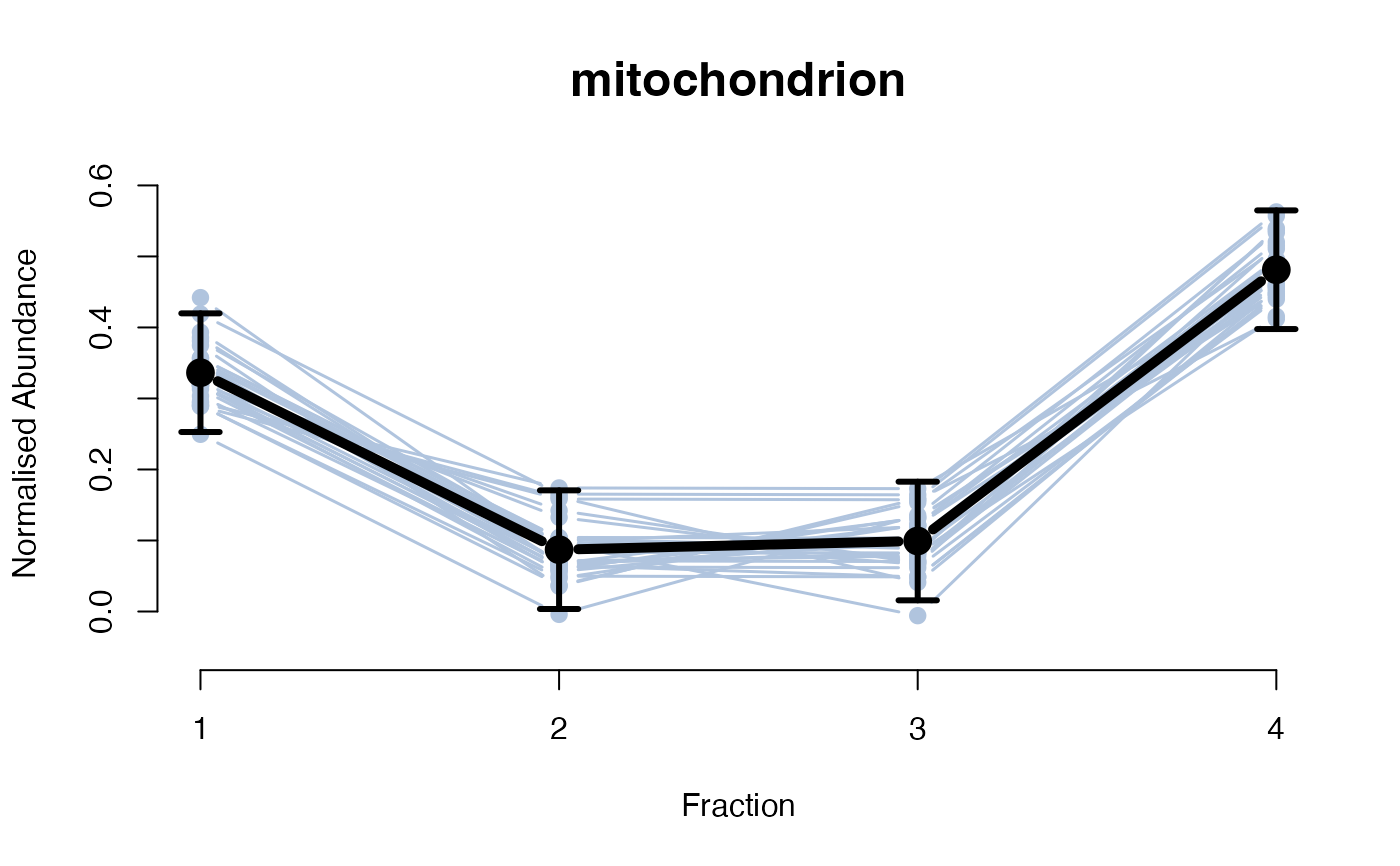
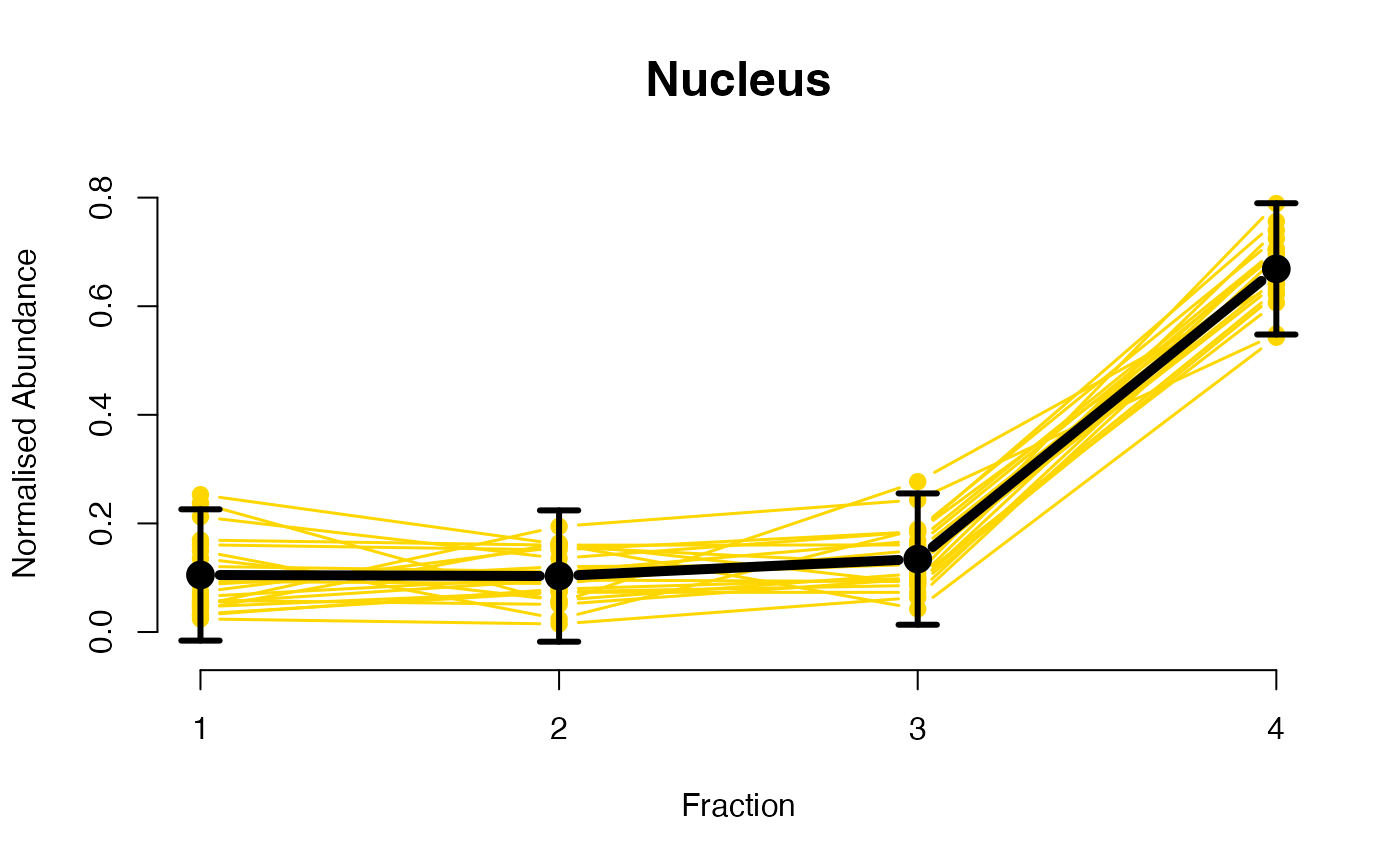
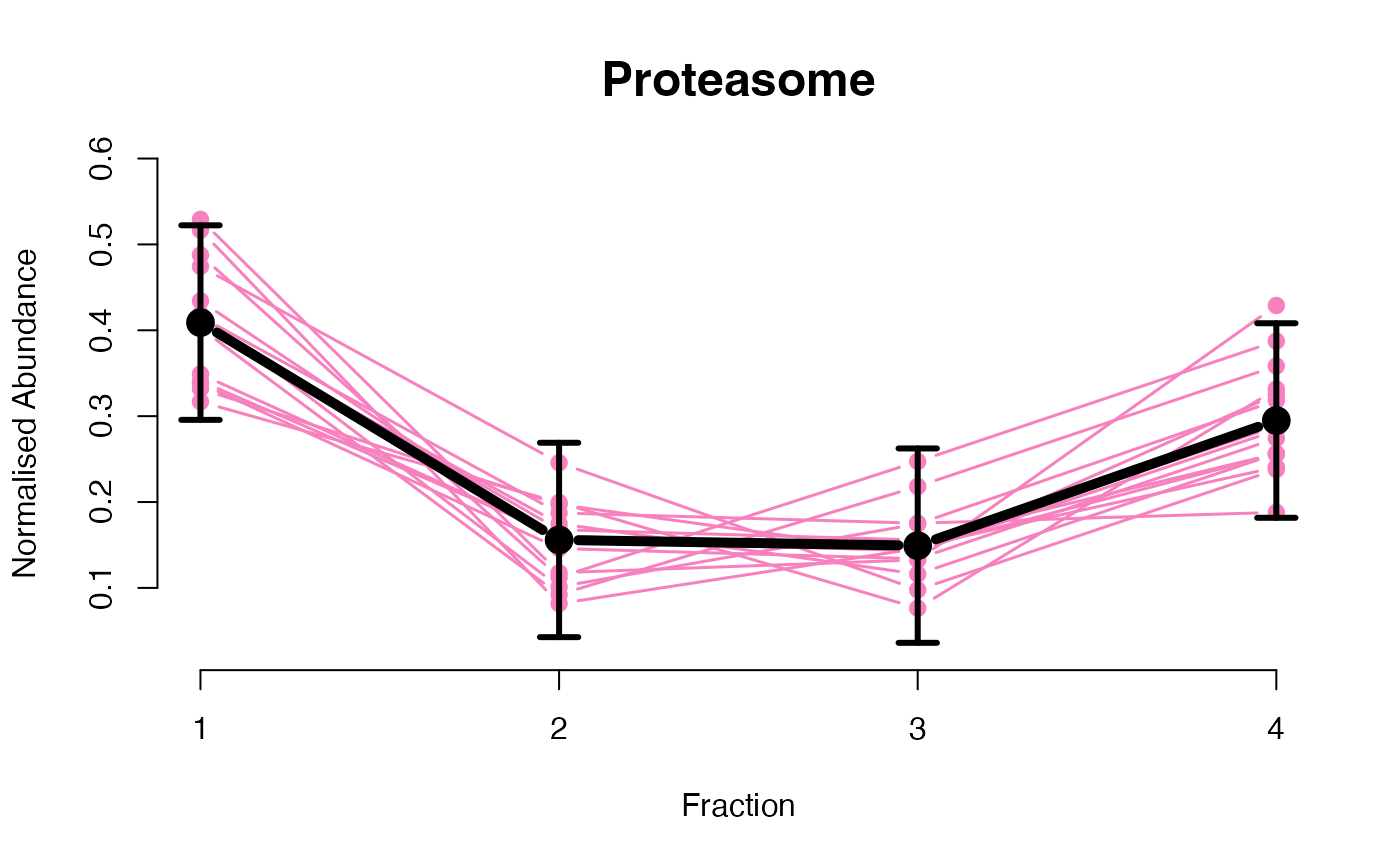
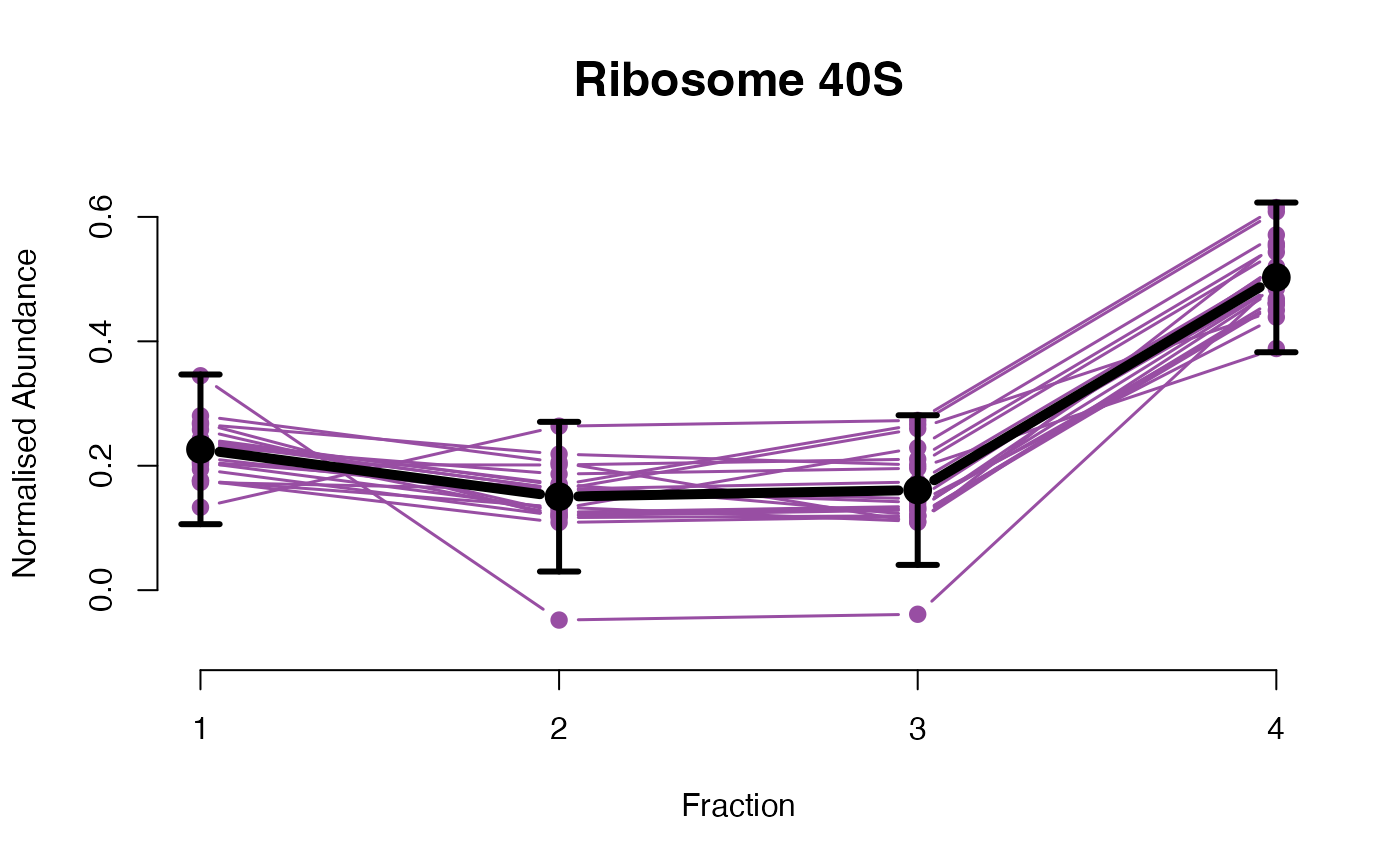
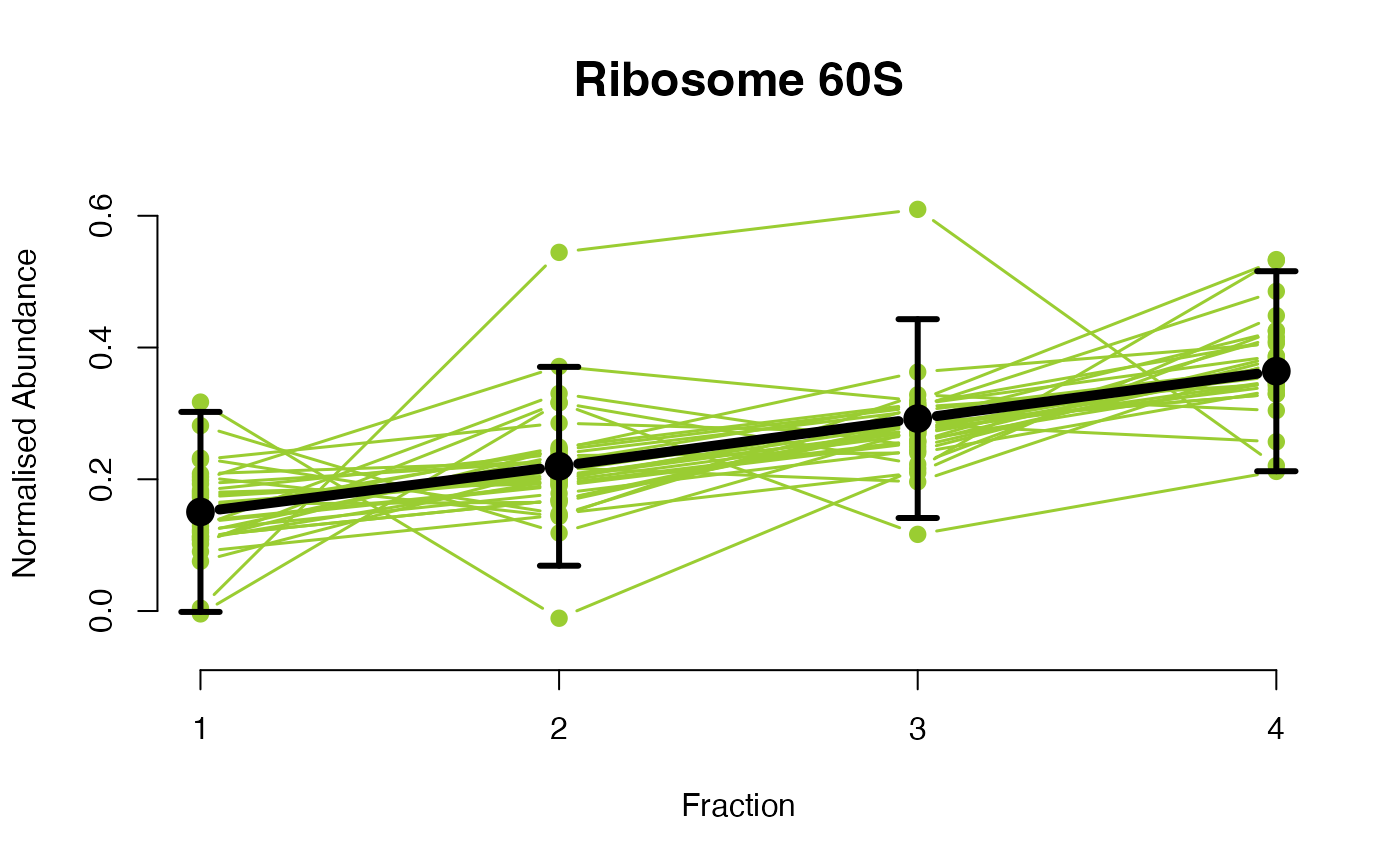
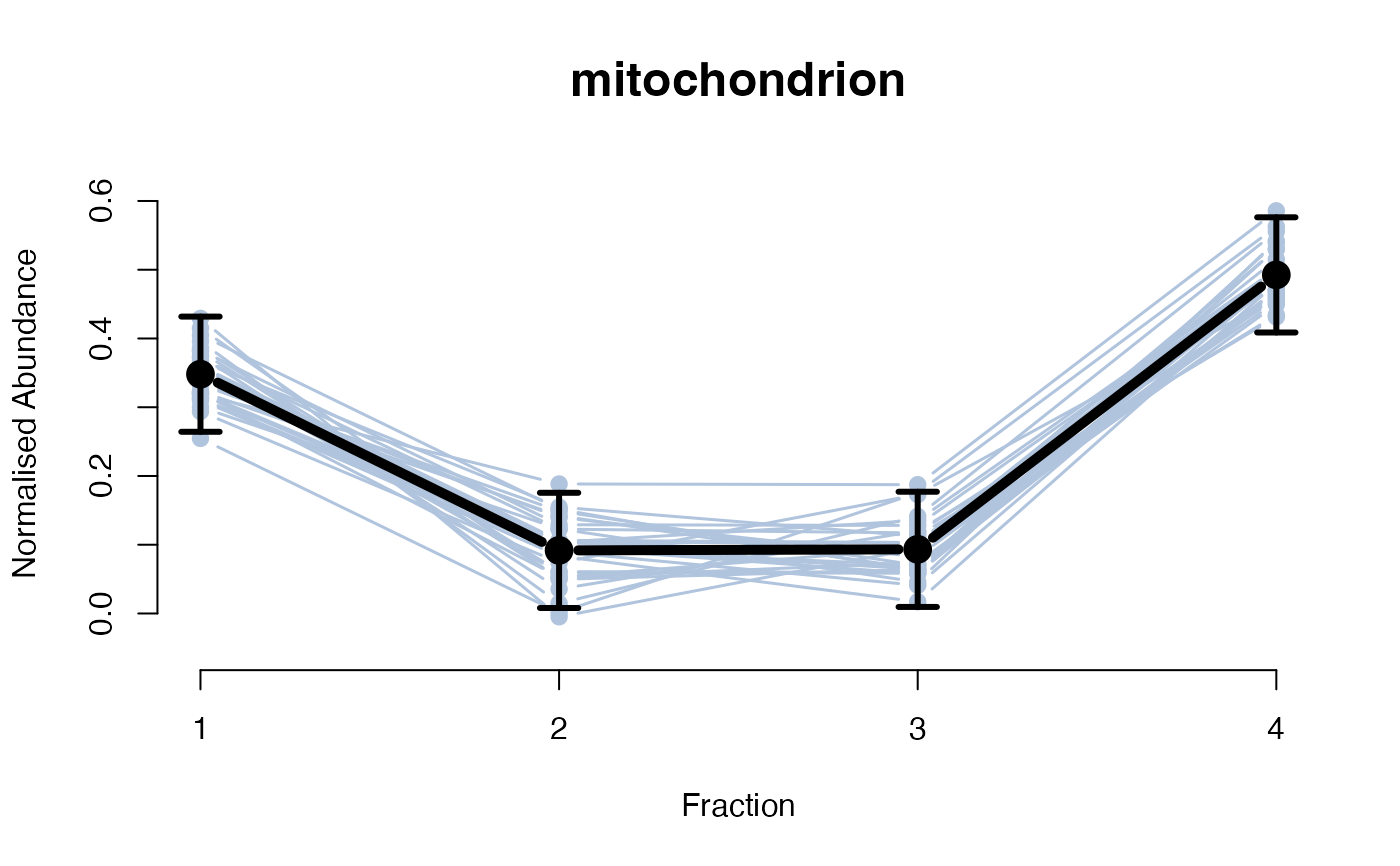
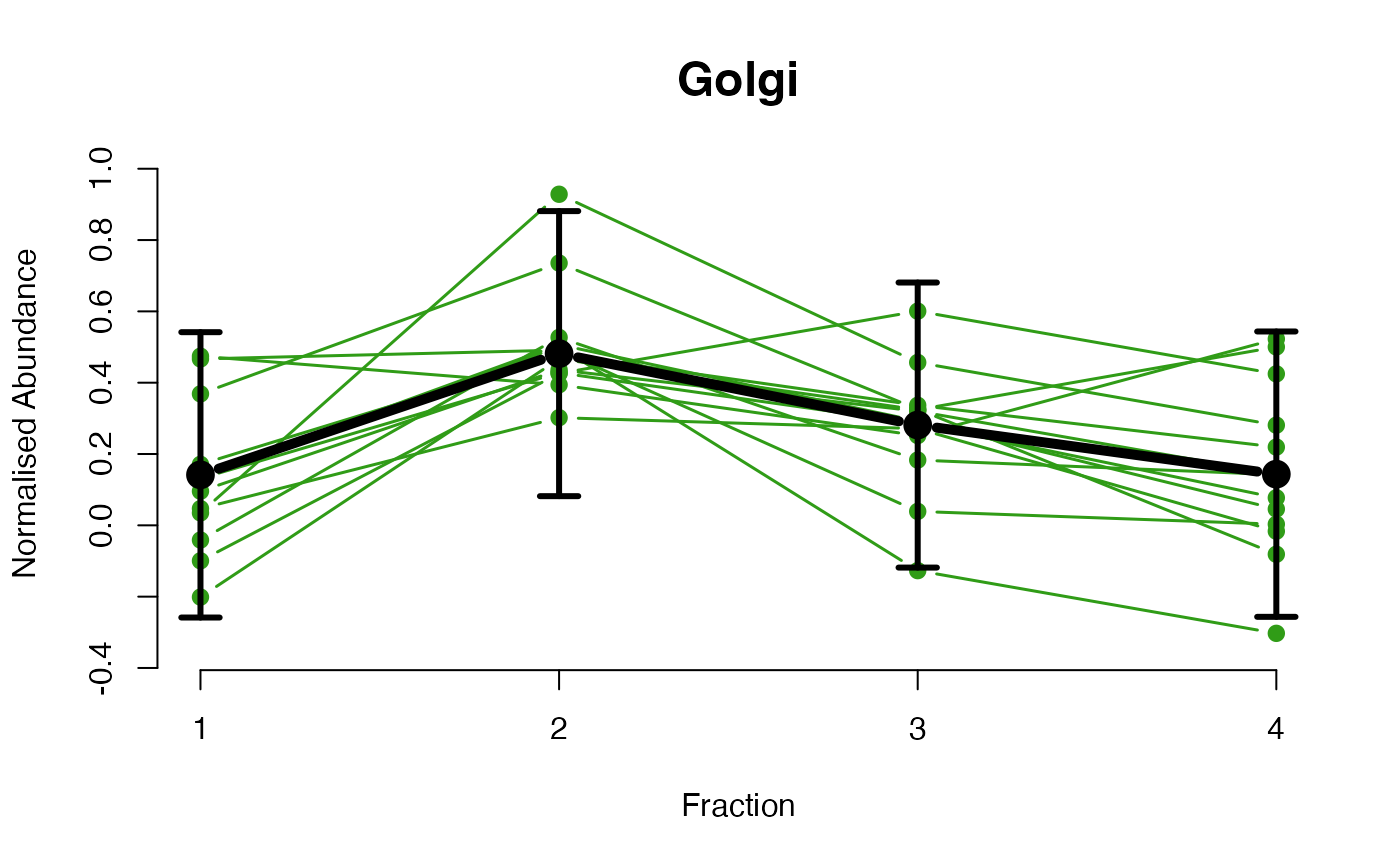
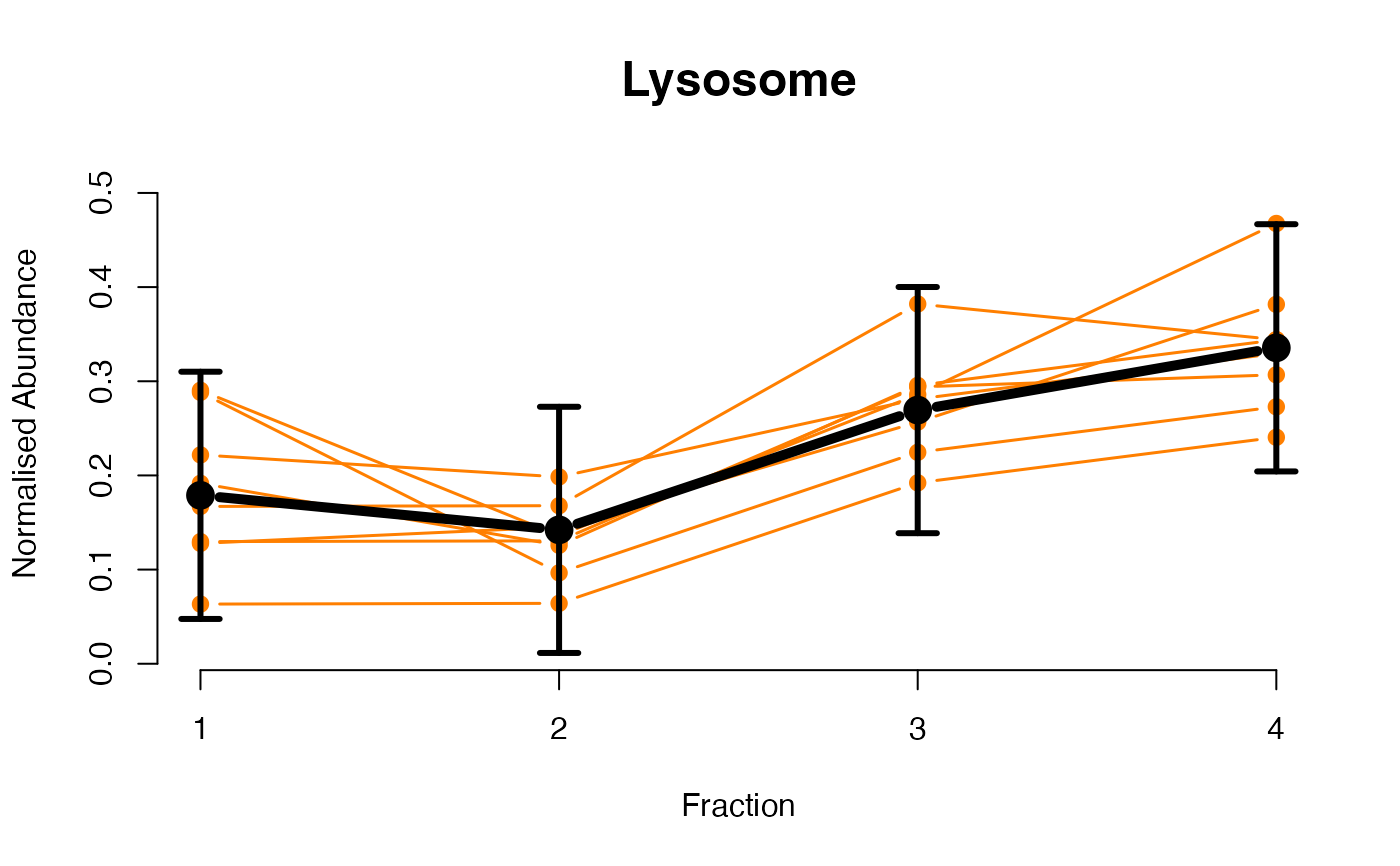
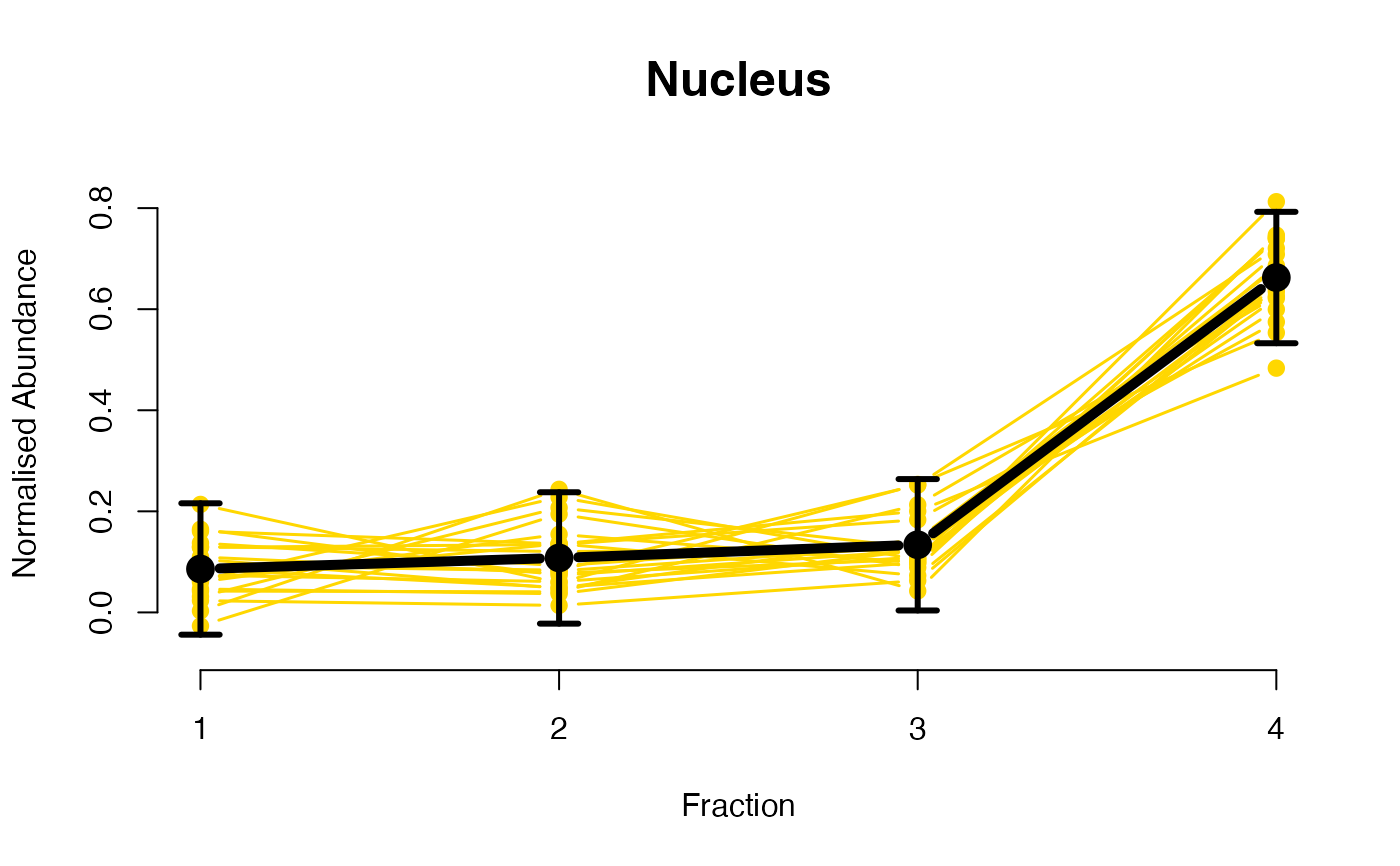
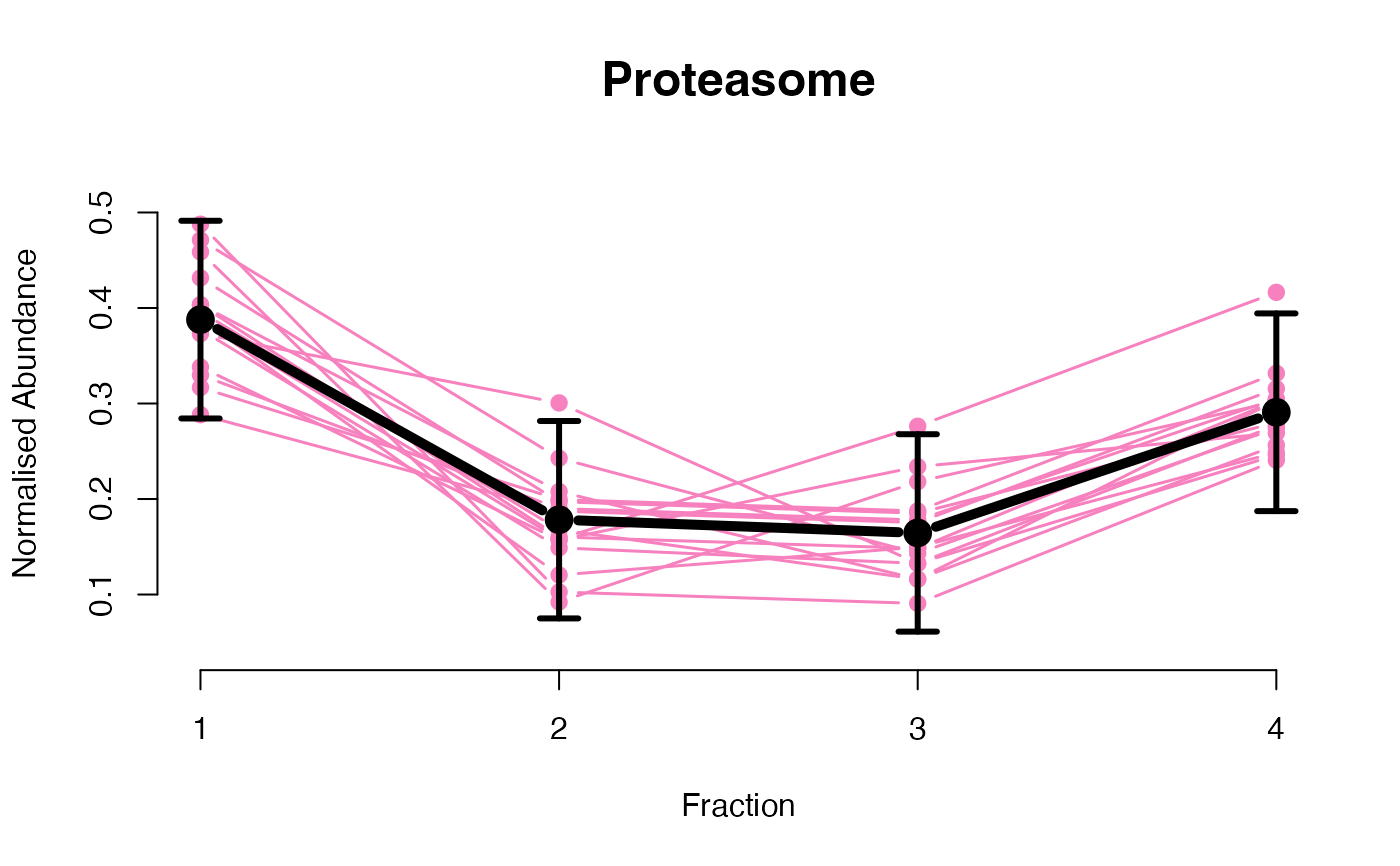
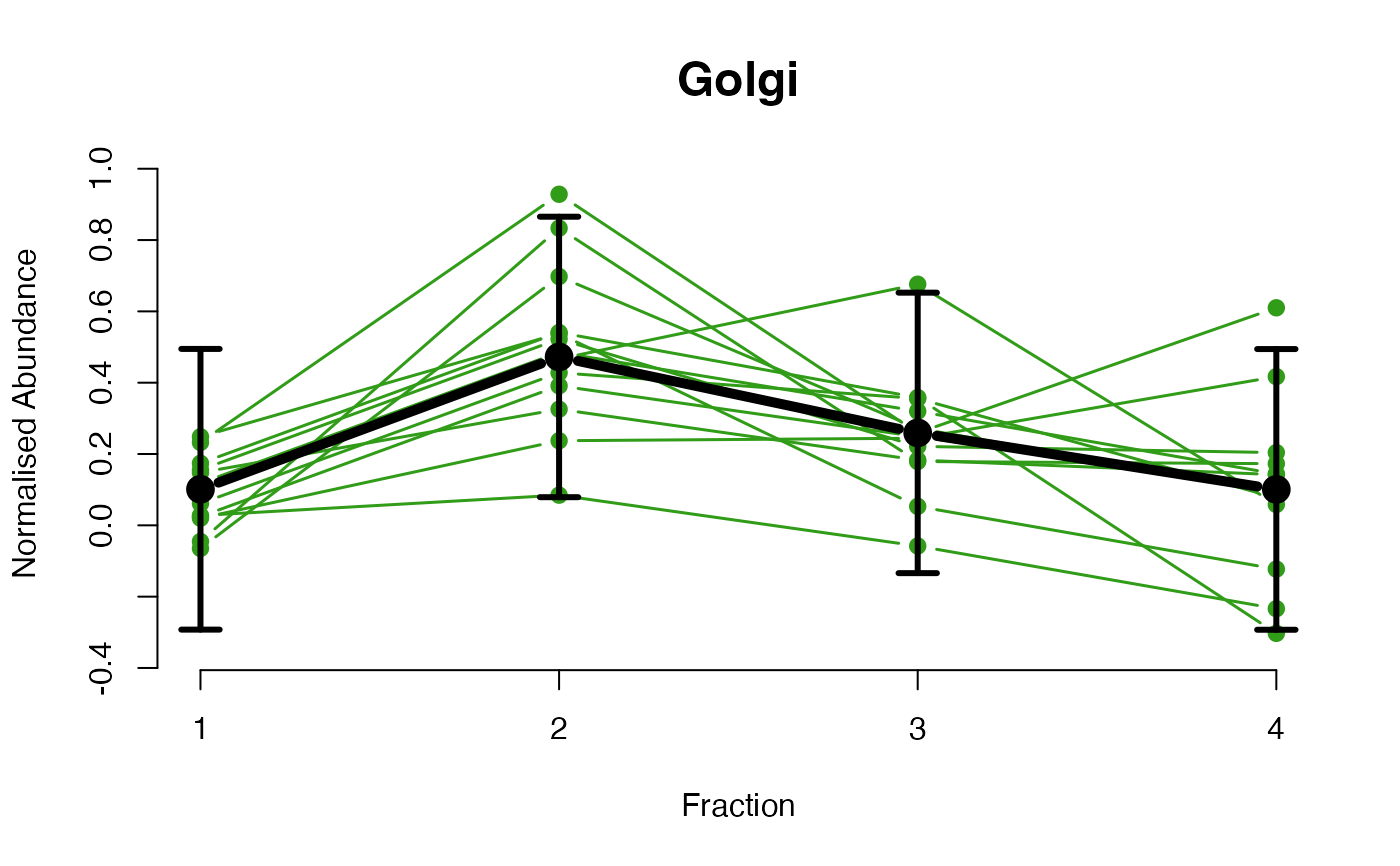
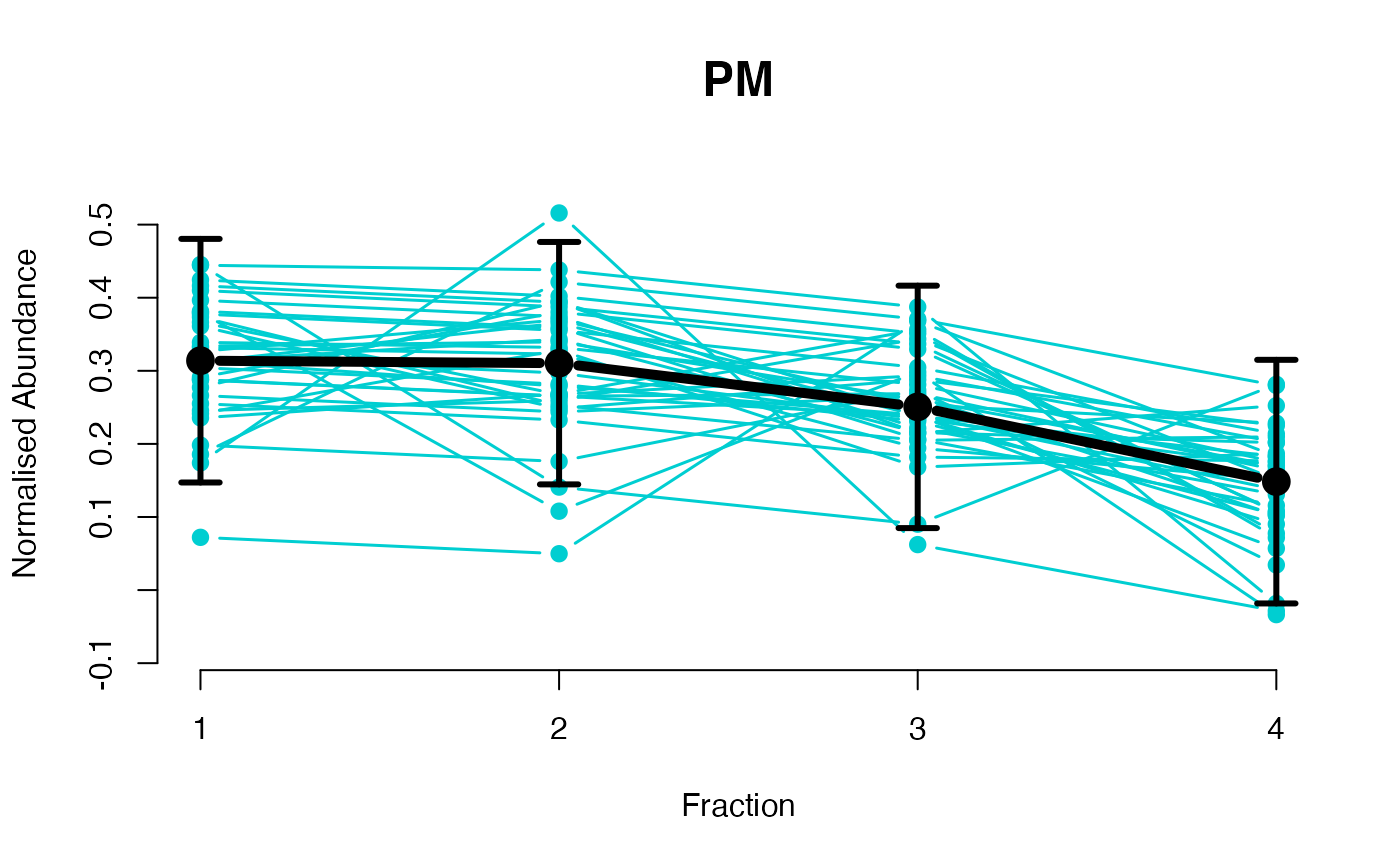
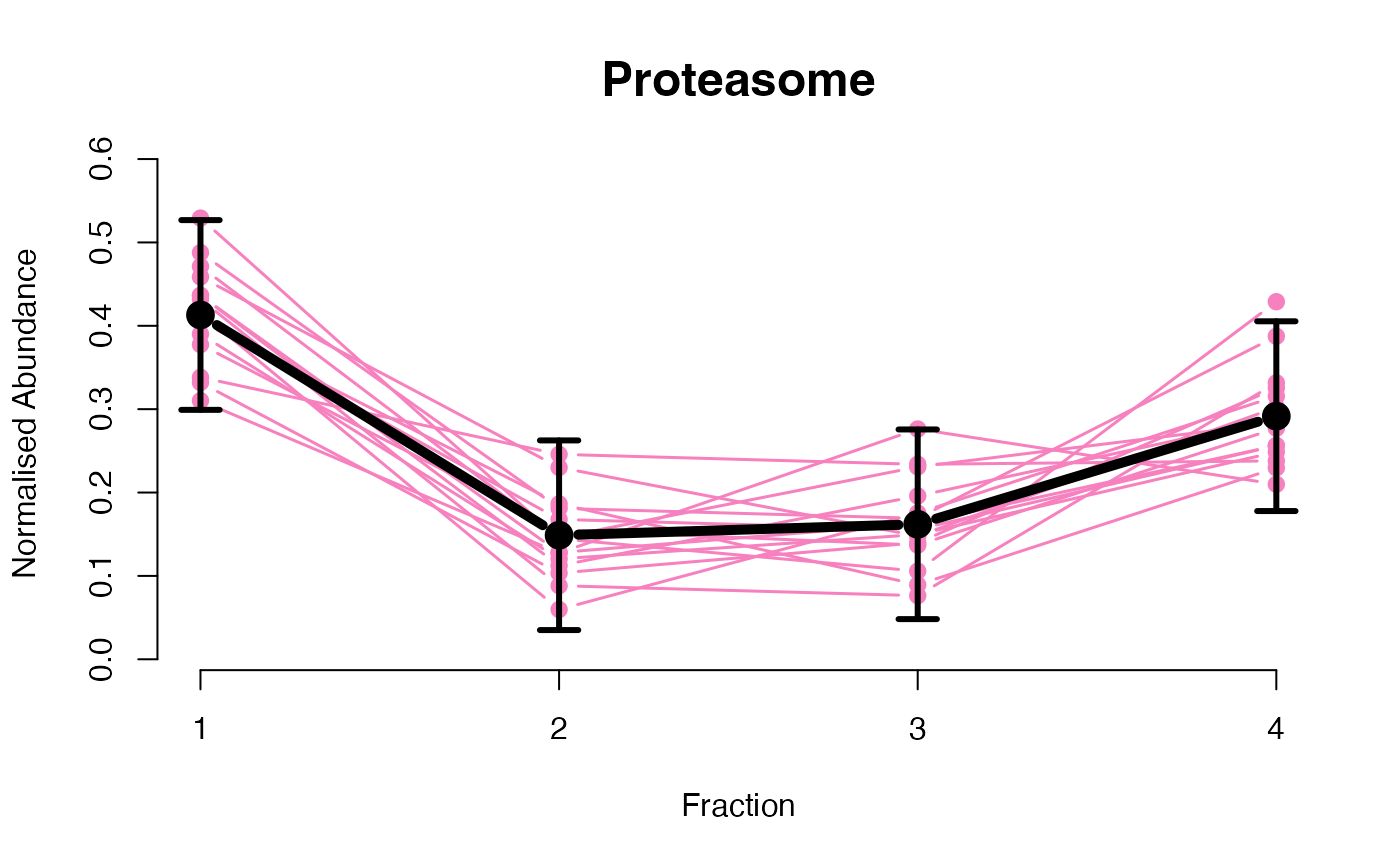
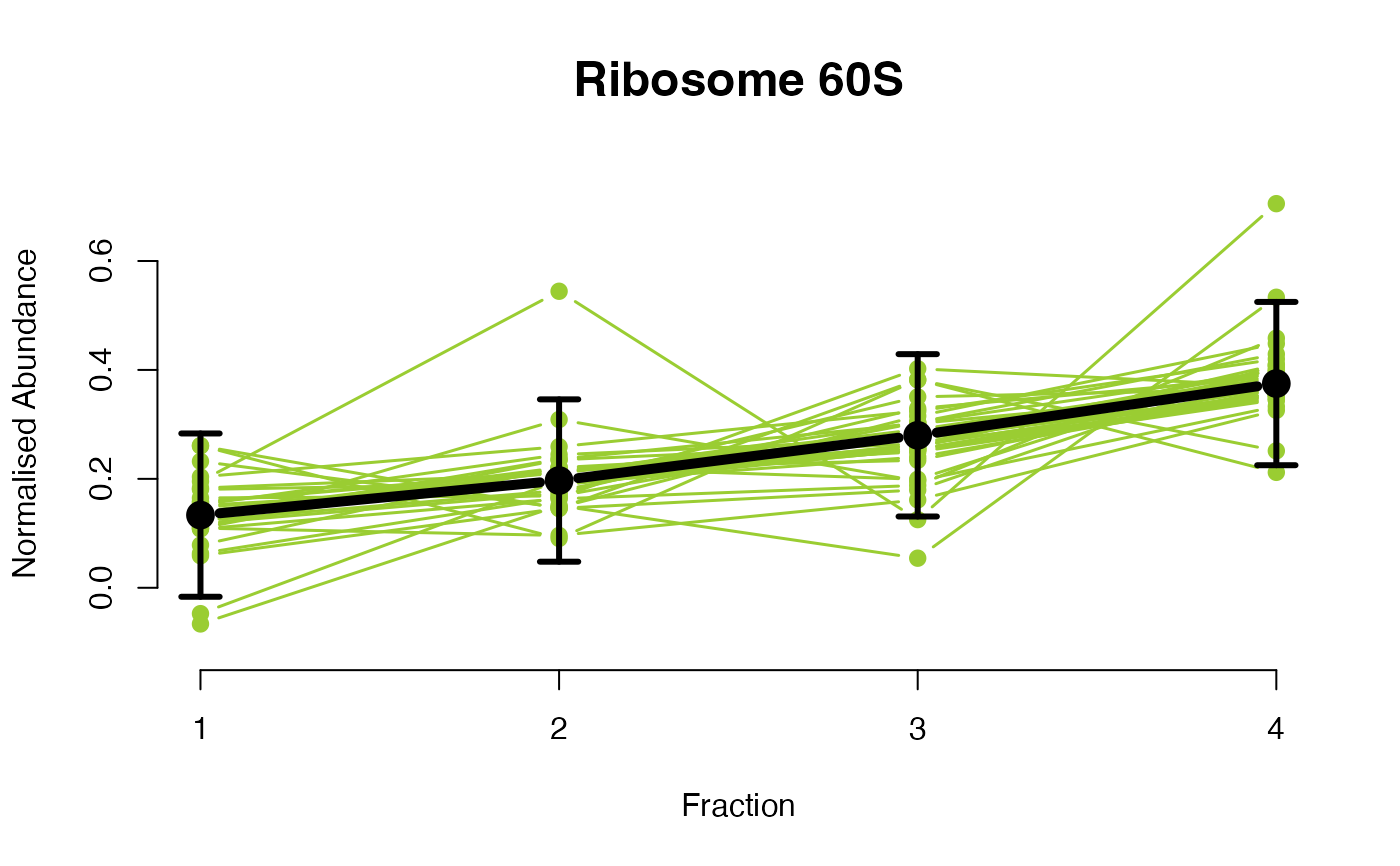
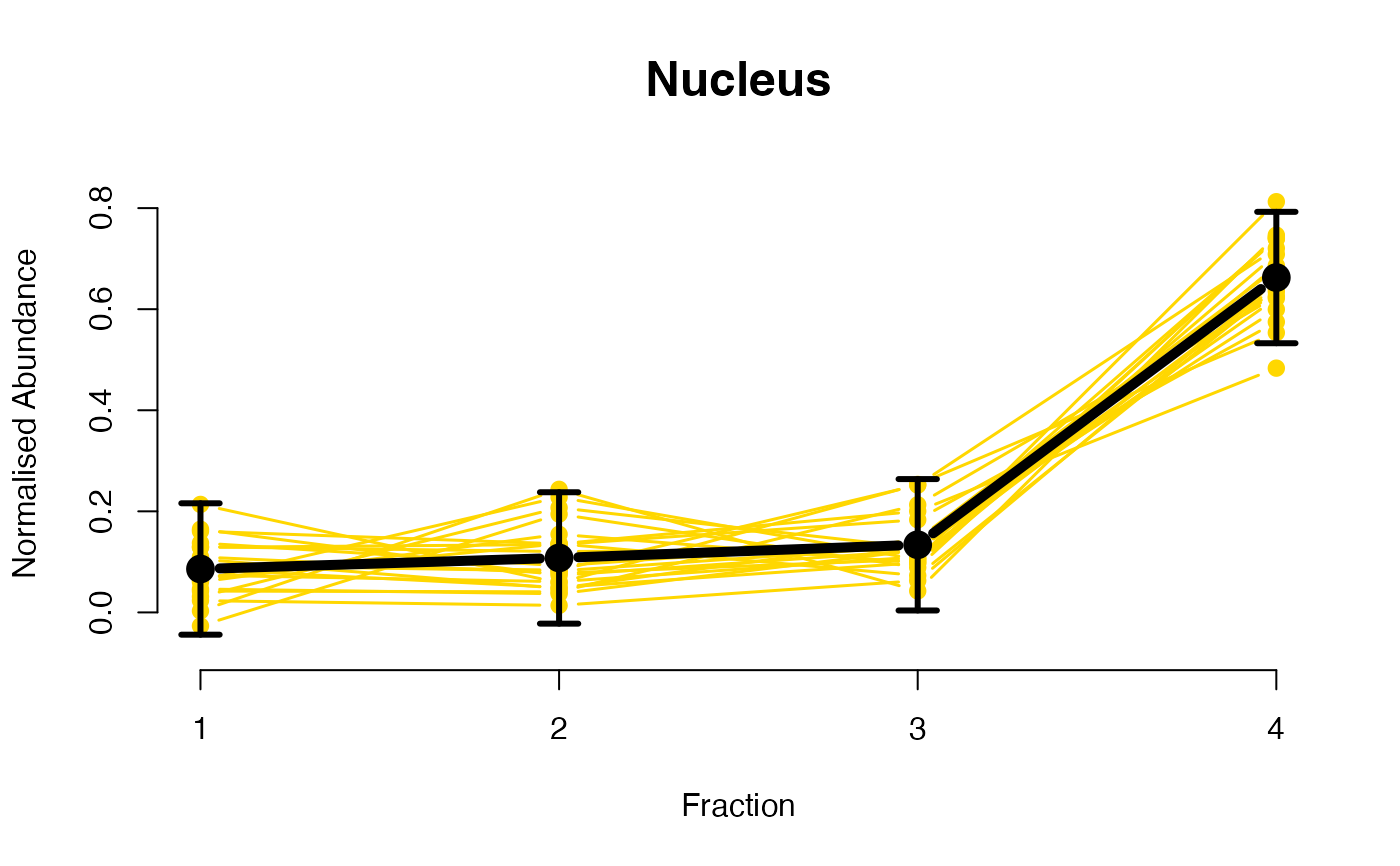
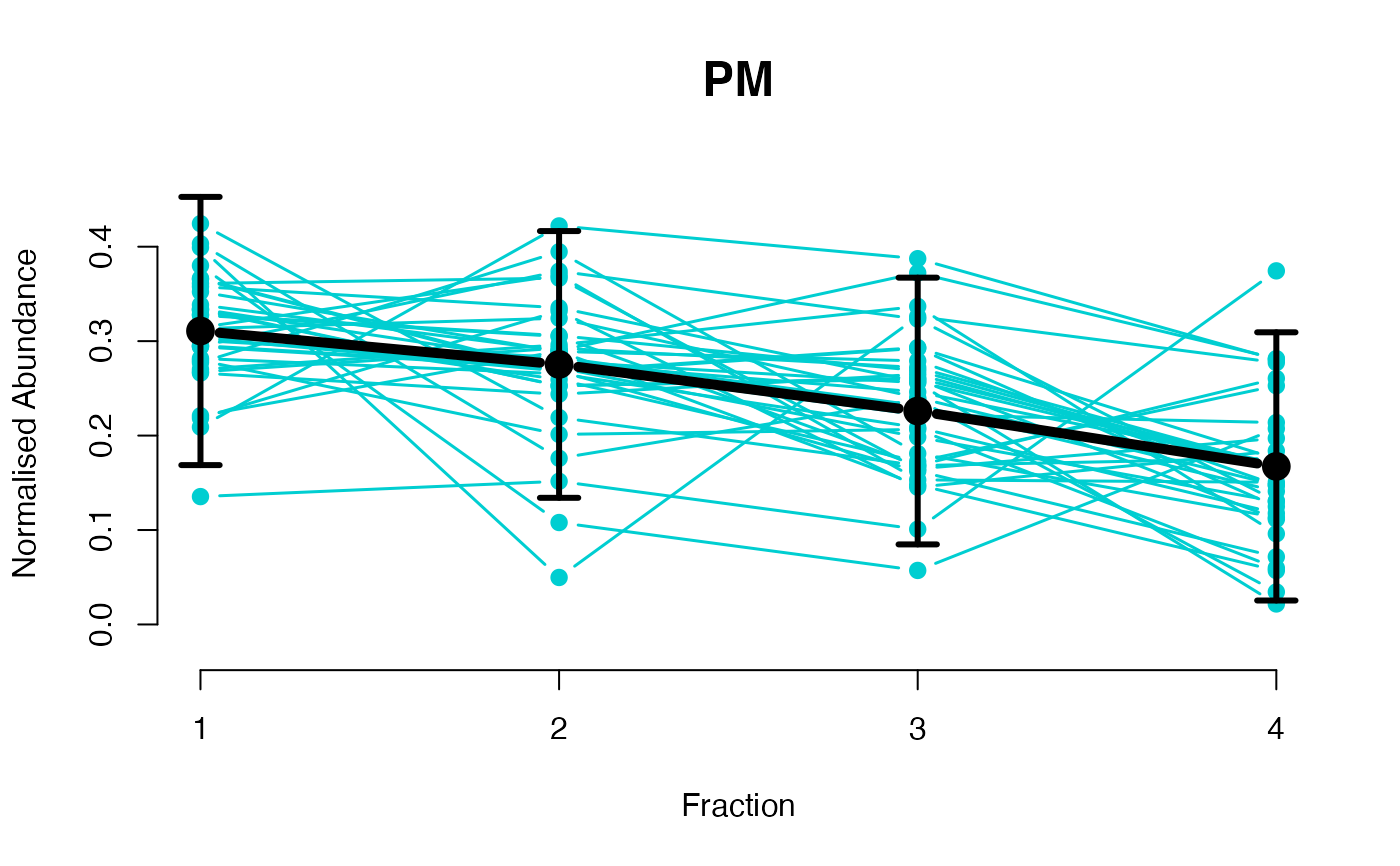
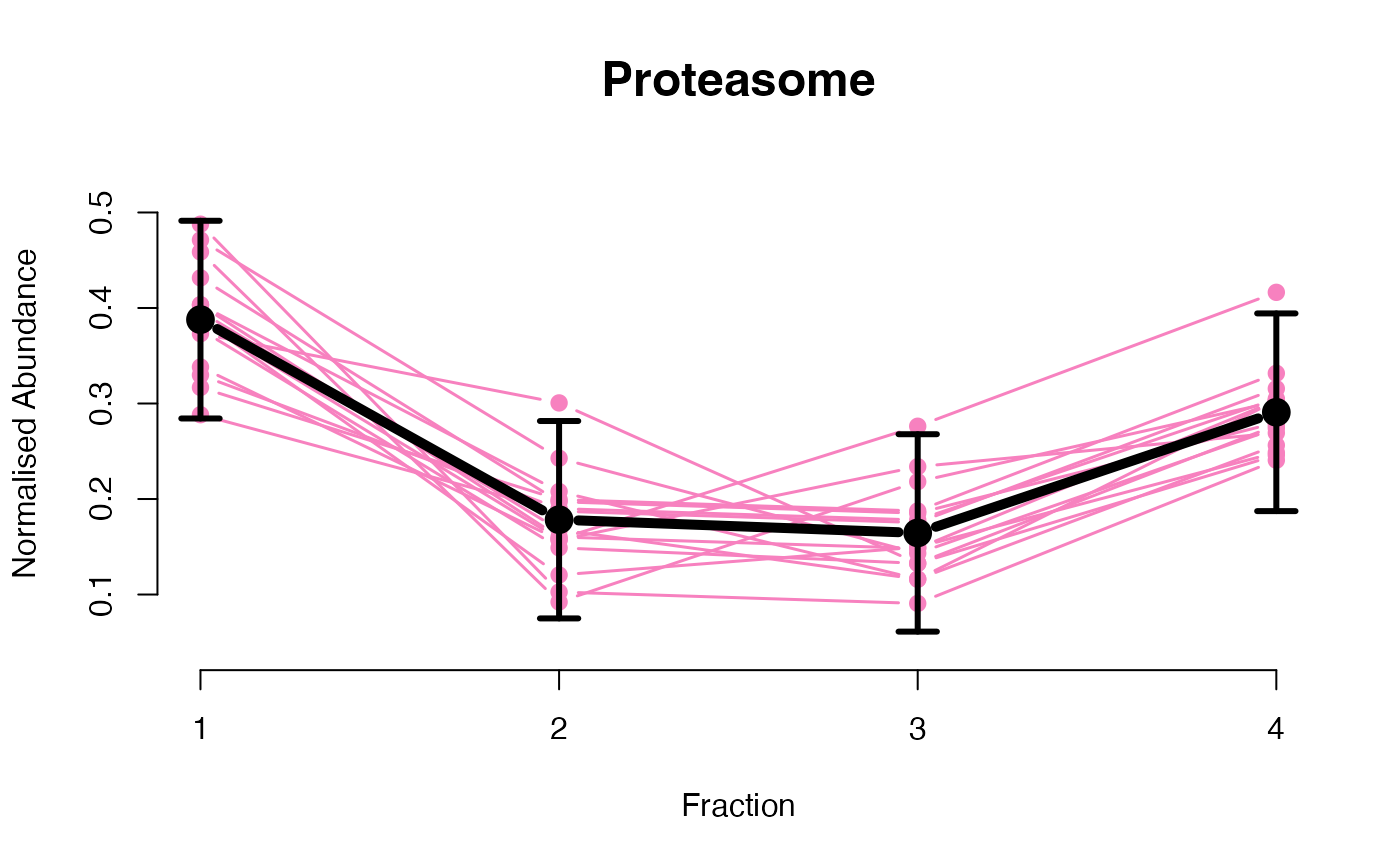
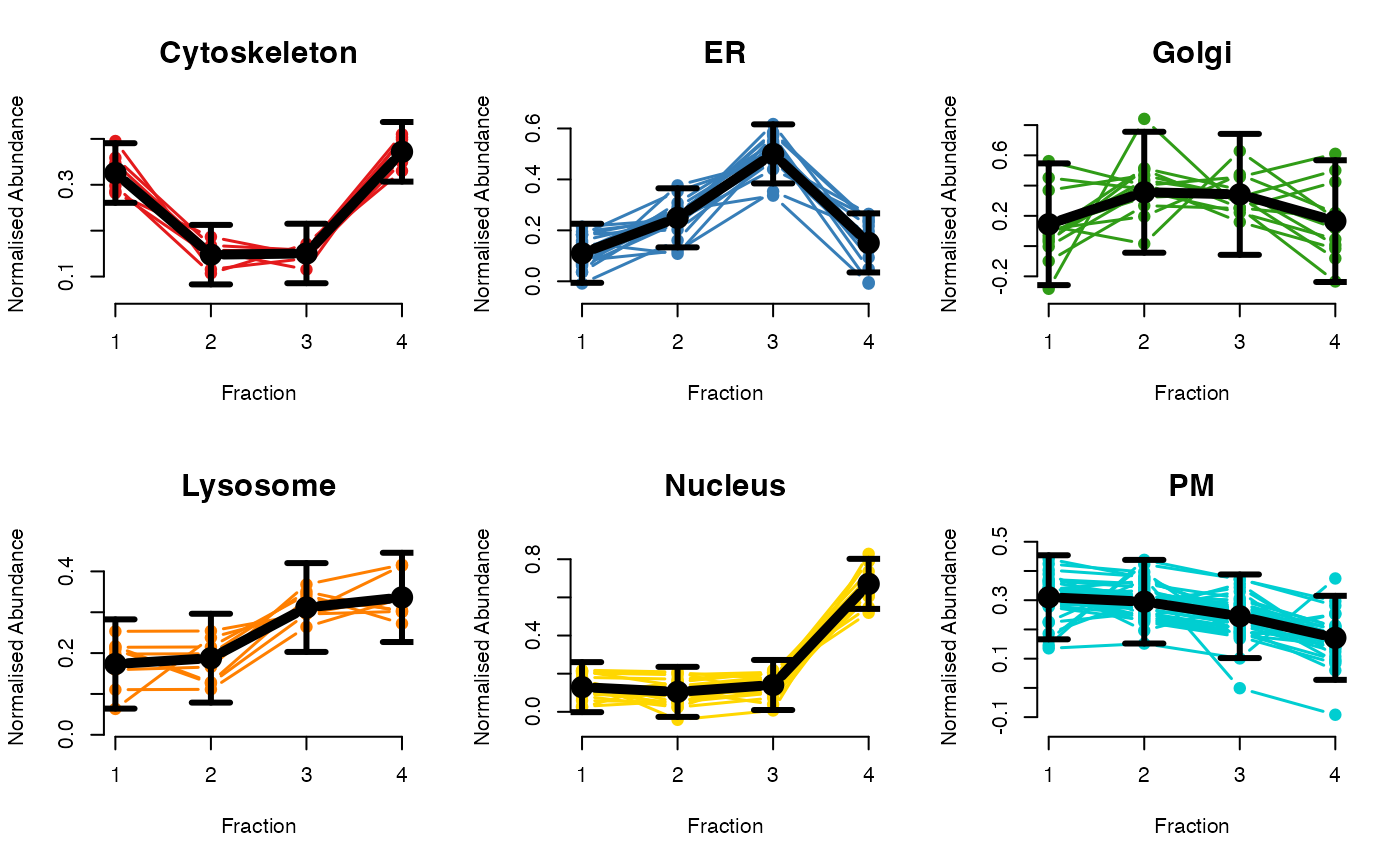
The functions plotGPmatern plot the posterior
predictives overlayed with the markers for each subcellular class.
Details
This set of functions allow users to fit GPs to their data. The
fitGPmaternPC function allows users to pass a vector of penalised
complexity hyperparameters using the hyppar argument. You must
provide a matrix with 3 columns and 1 row. The order of these 3 columns
represent the hyperparameters length-scale, amplitude, variance. We have
found that the matrix(c(10, 60, 250), nrow = 1) worked well for the
spatial proteomics datasets tested in Crook et al (2021). This was visually
assessed by passing these values and visualising the GP fit using the
plotGPmatern function (please see vignette for an example of the
output). Generally, (1) increasing the lengthscale parameter (the first
column of the hyppar matrix) increases the spread of the covariance
i.e. the similarity between points, (2) increasing the amplitude parameter
(the second column of the hyppar matrix) increases the maximum value
of the covariance and lastly (3) decreasing the variance (third column of
the hyppar matrix) reduces the smoothness of the function to allow
for local variations. We strongly recommend users start with the recommended
parameters and change and assess them as necessary for their dataset by
visually evaluating the fit of the GPs using the plotGPmatern
function. Please see the vignettes for more details and examples.
Examples
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
gpParams <- lapply(tansim$lopitrep, function(x) fitGP(x))



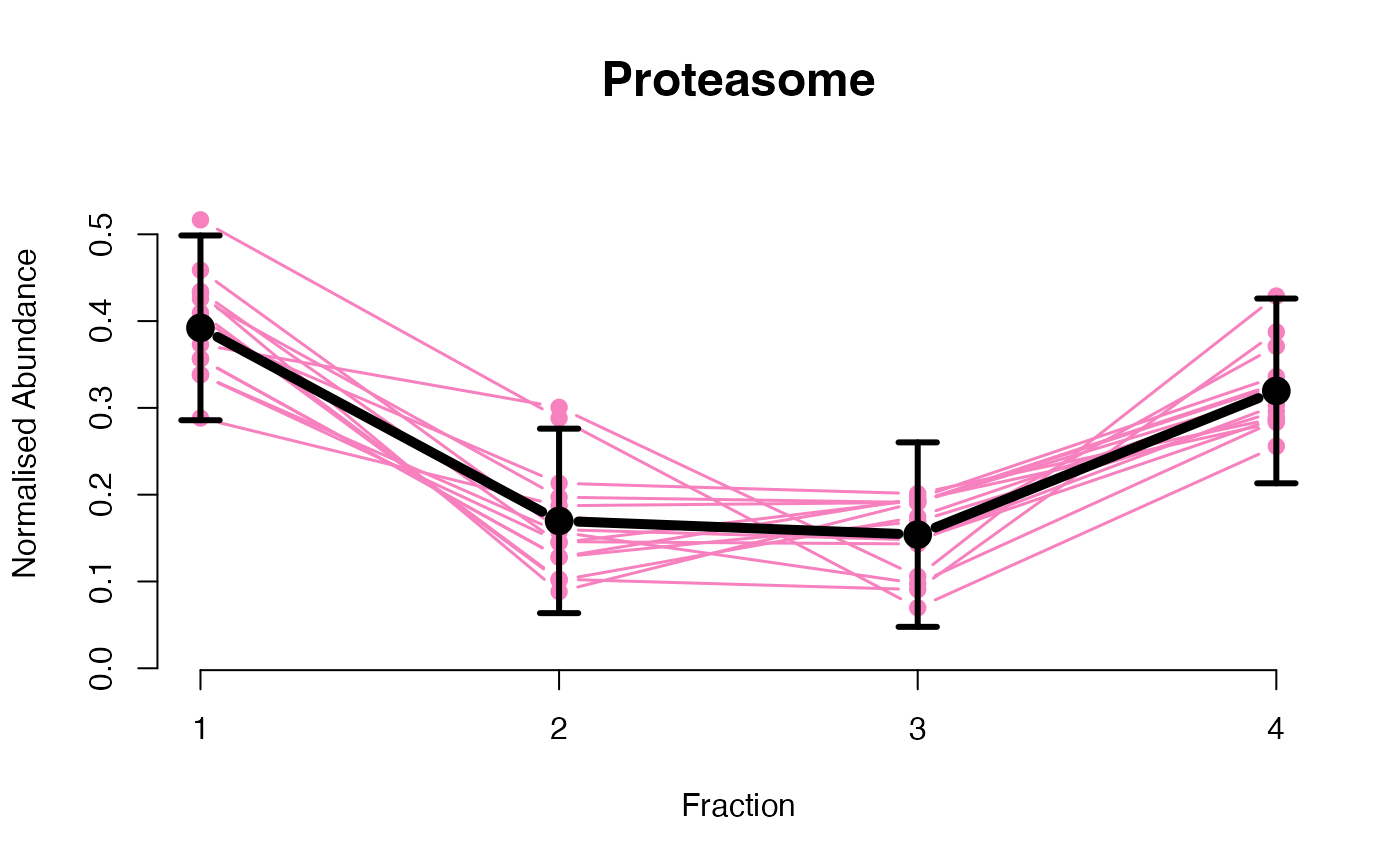



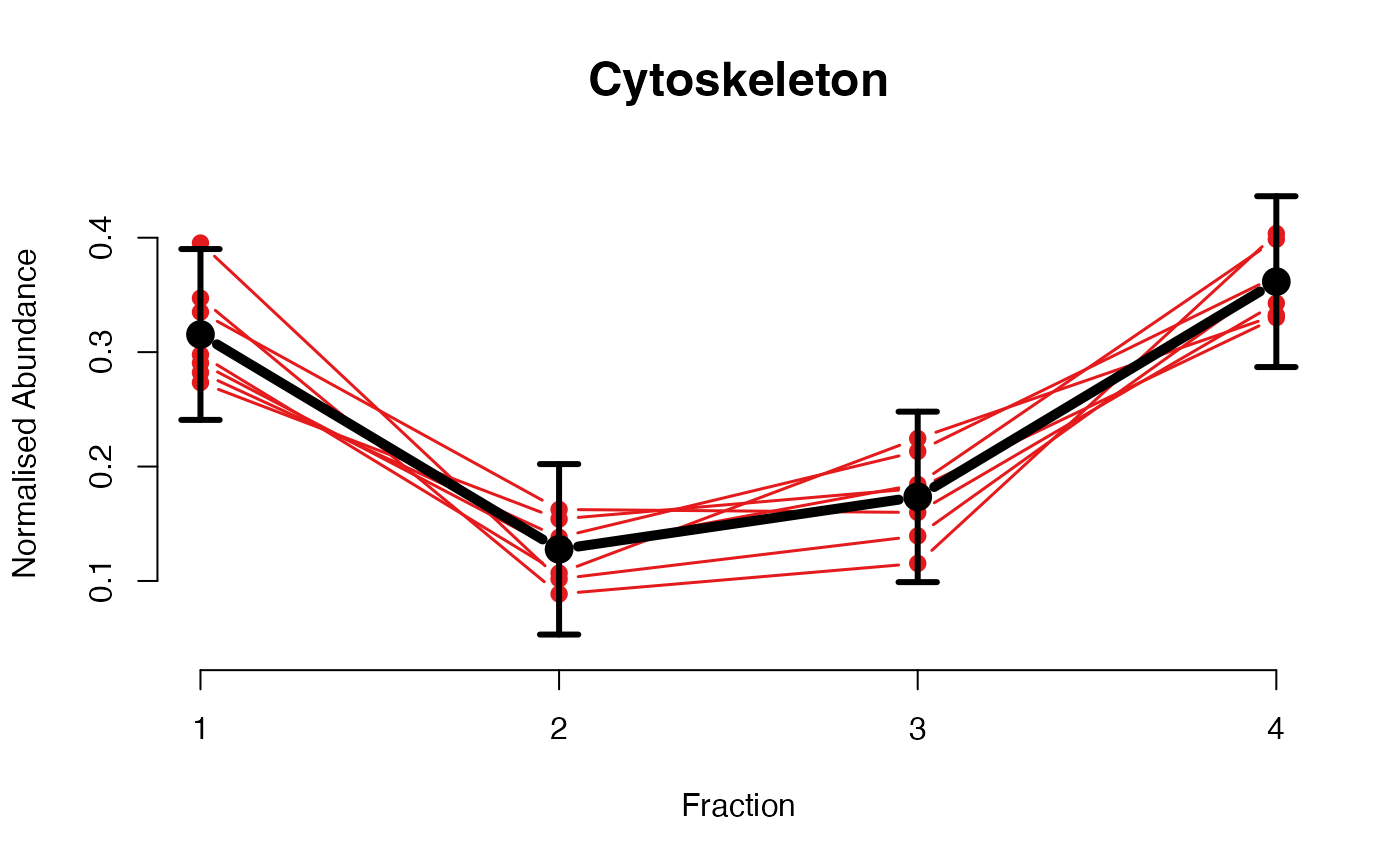
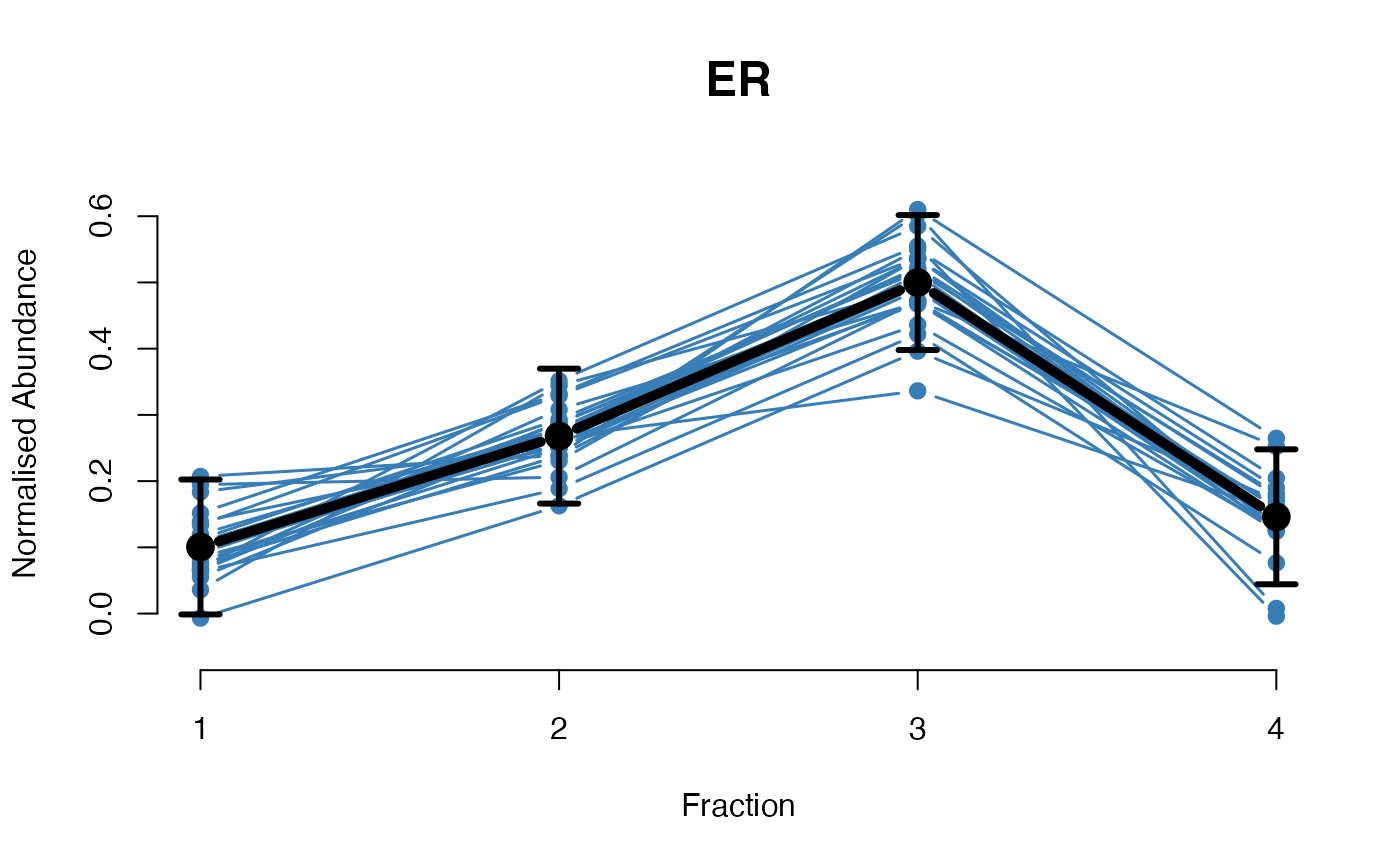
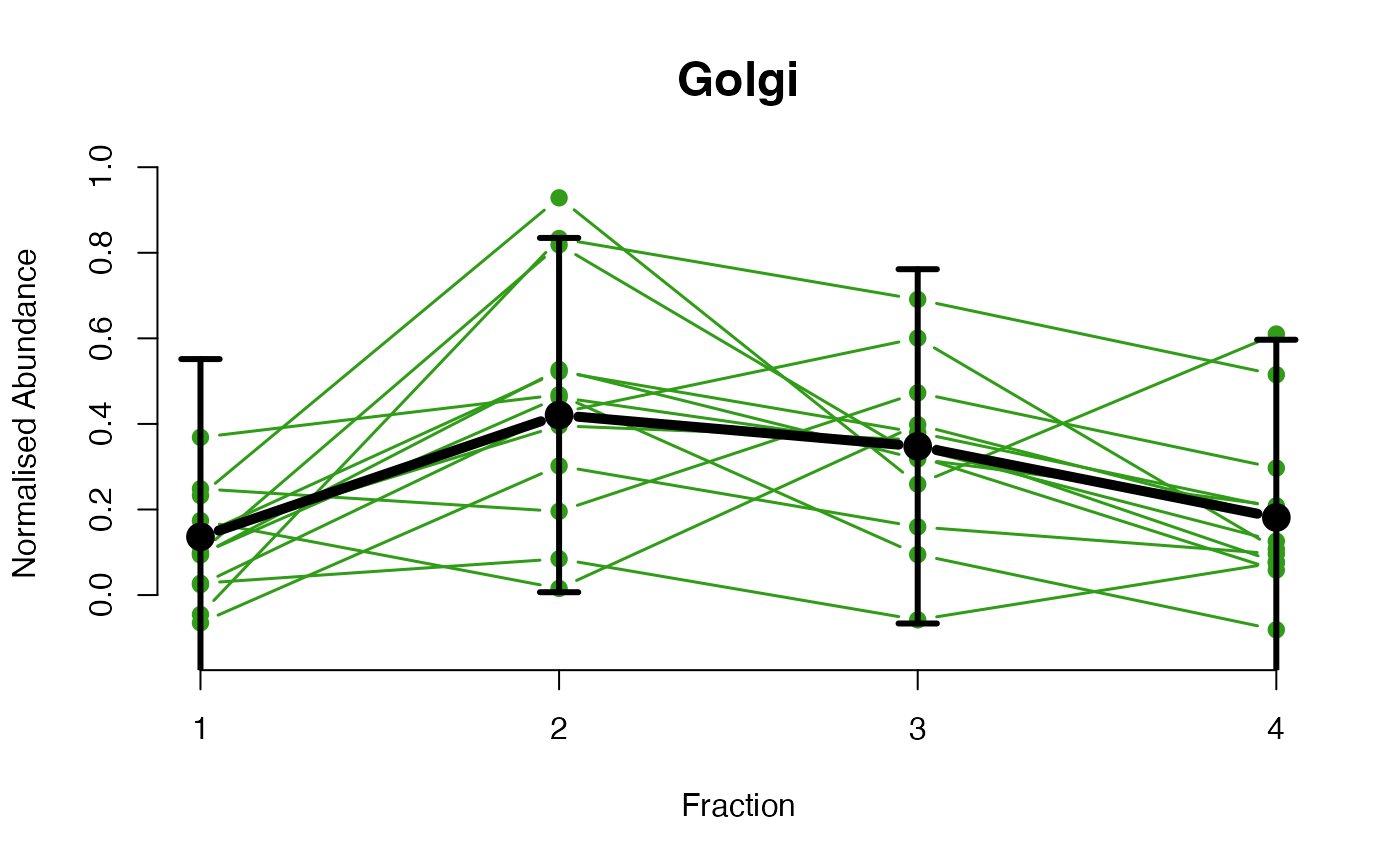
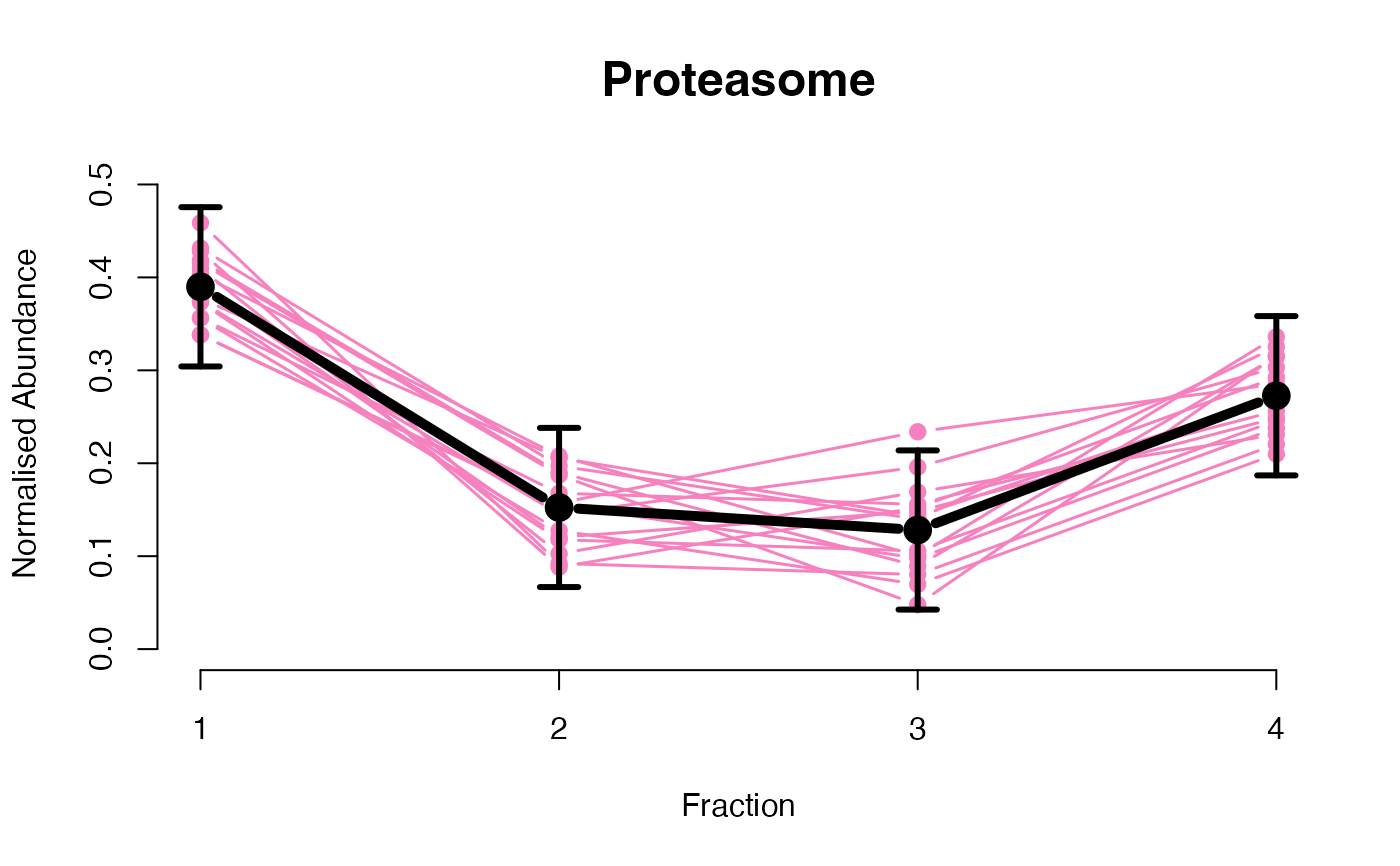
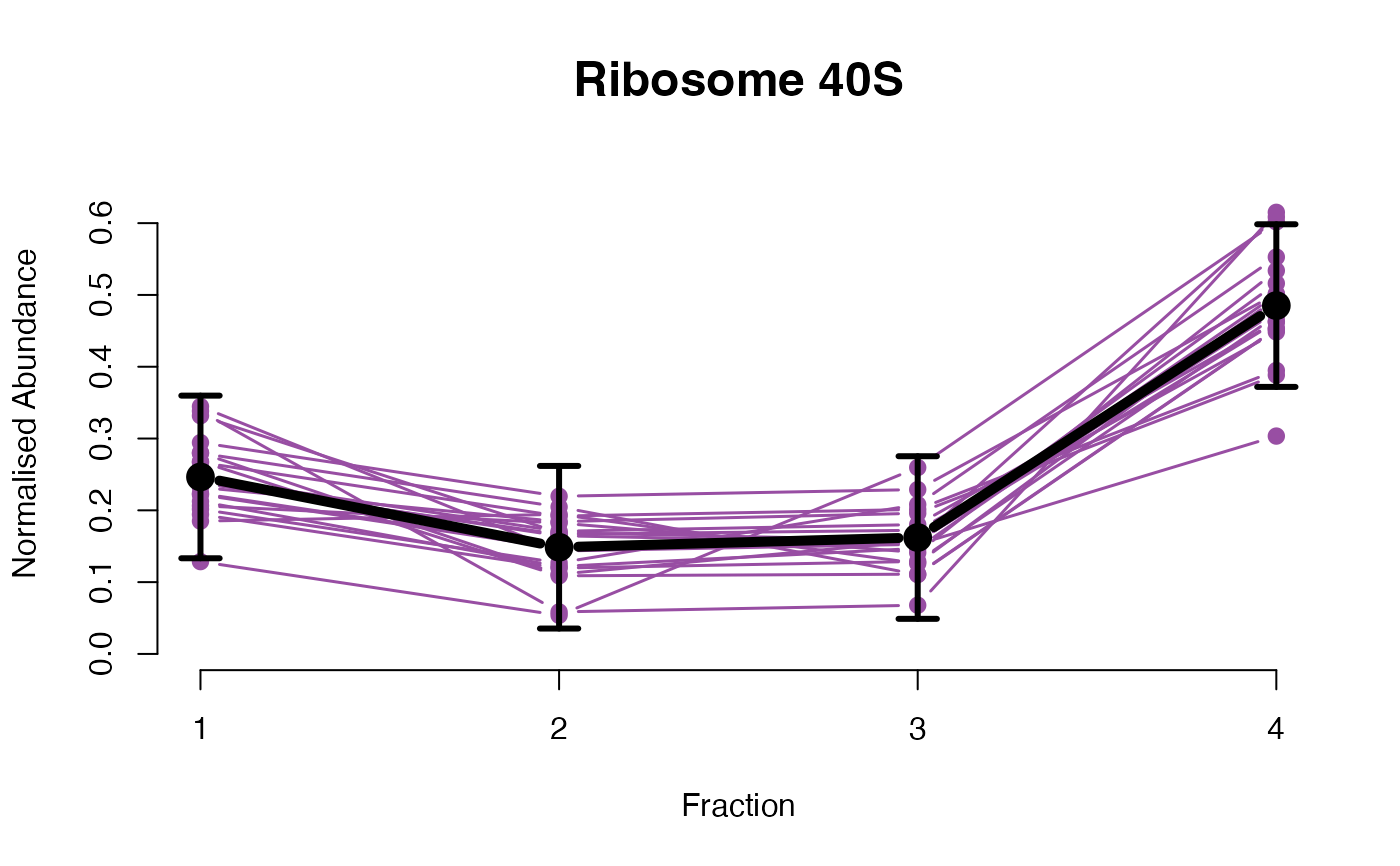

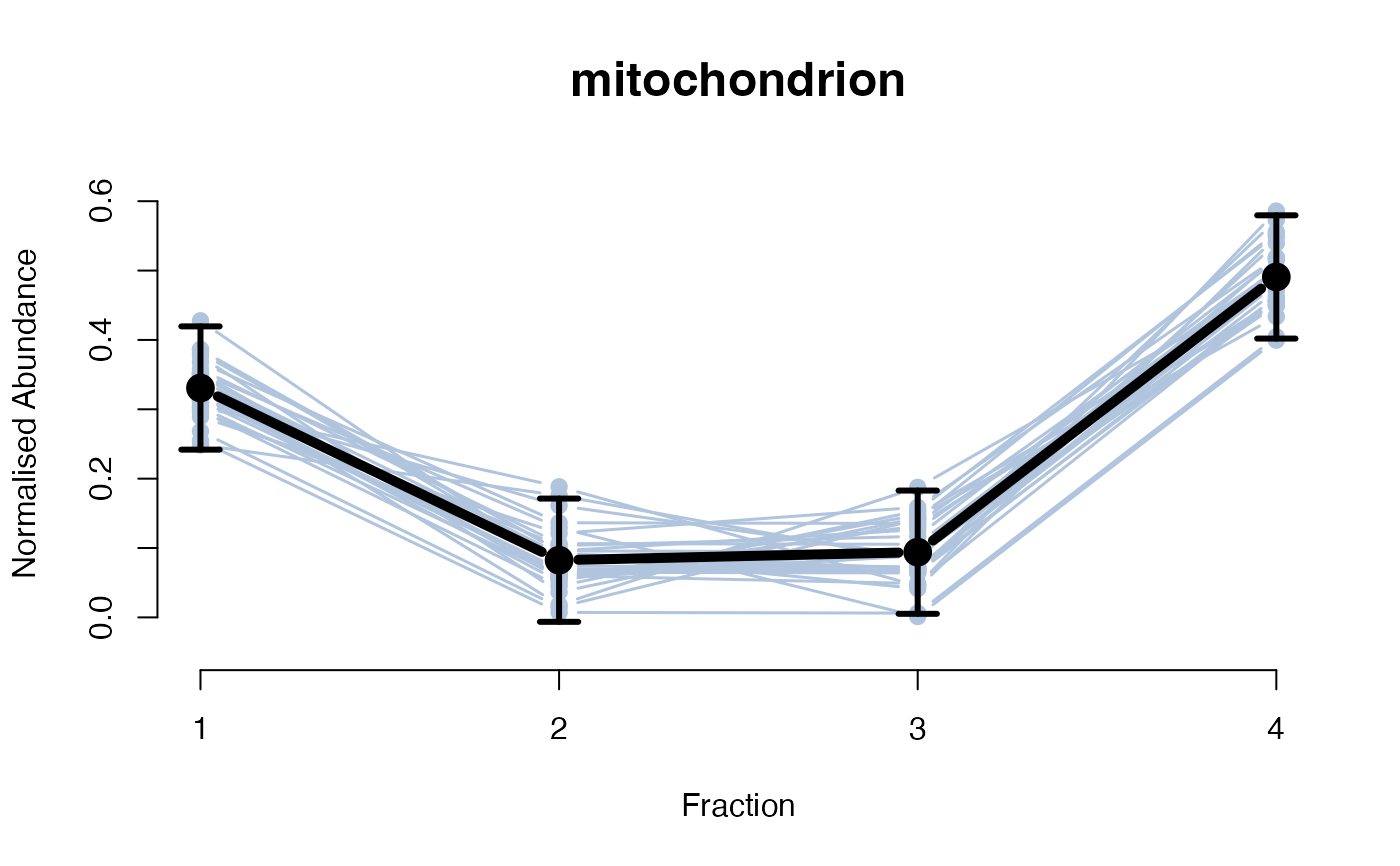

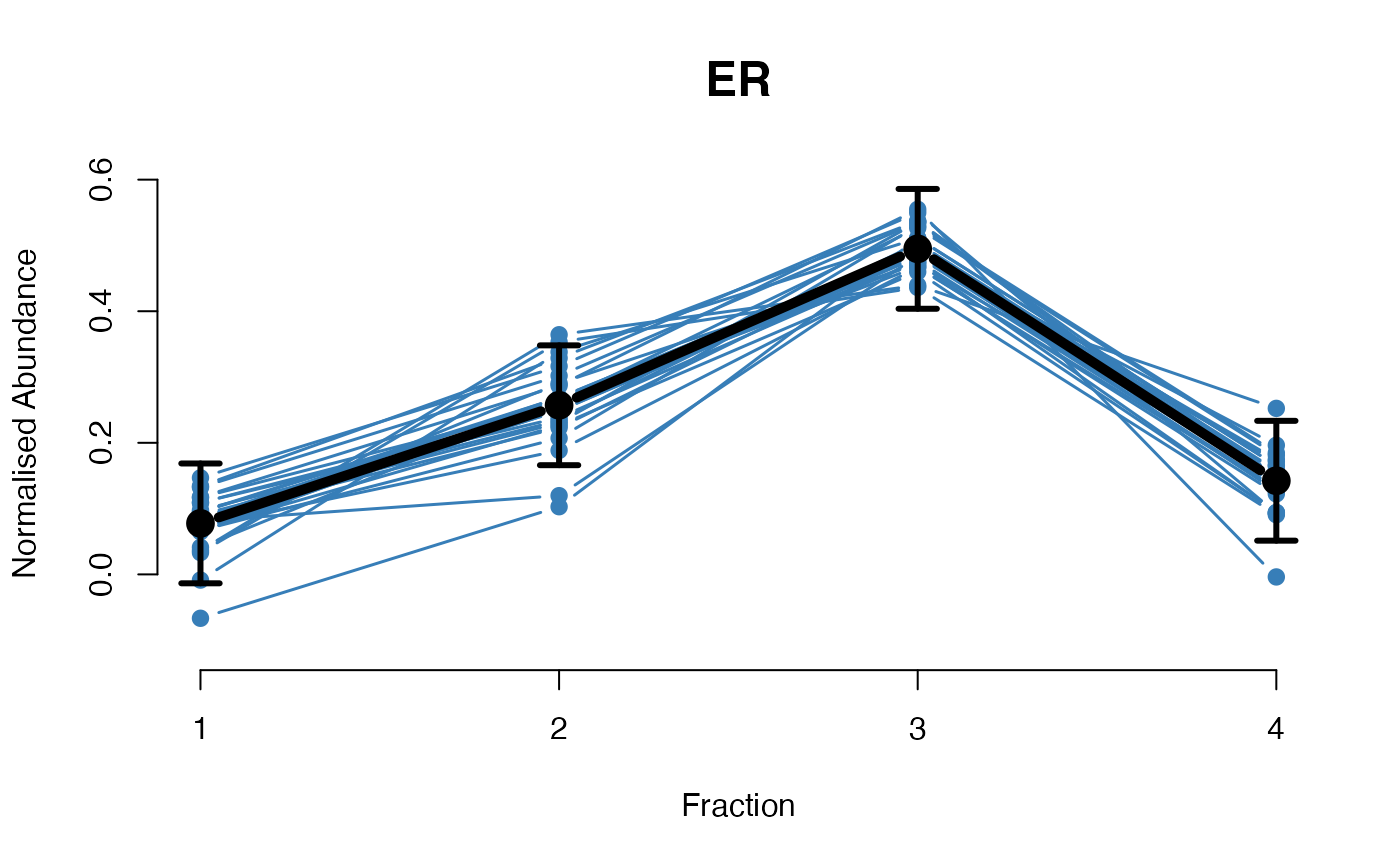

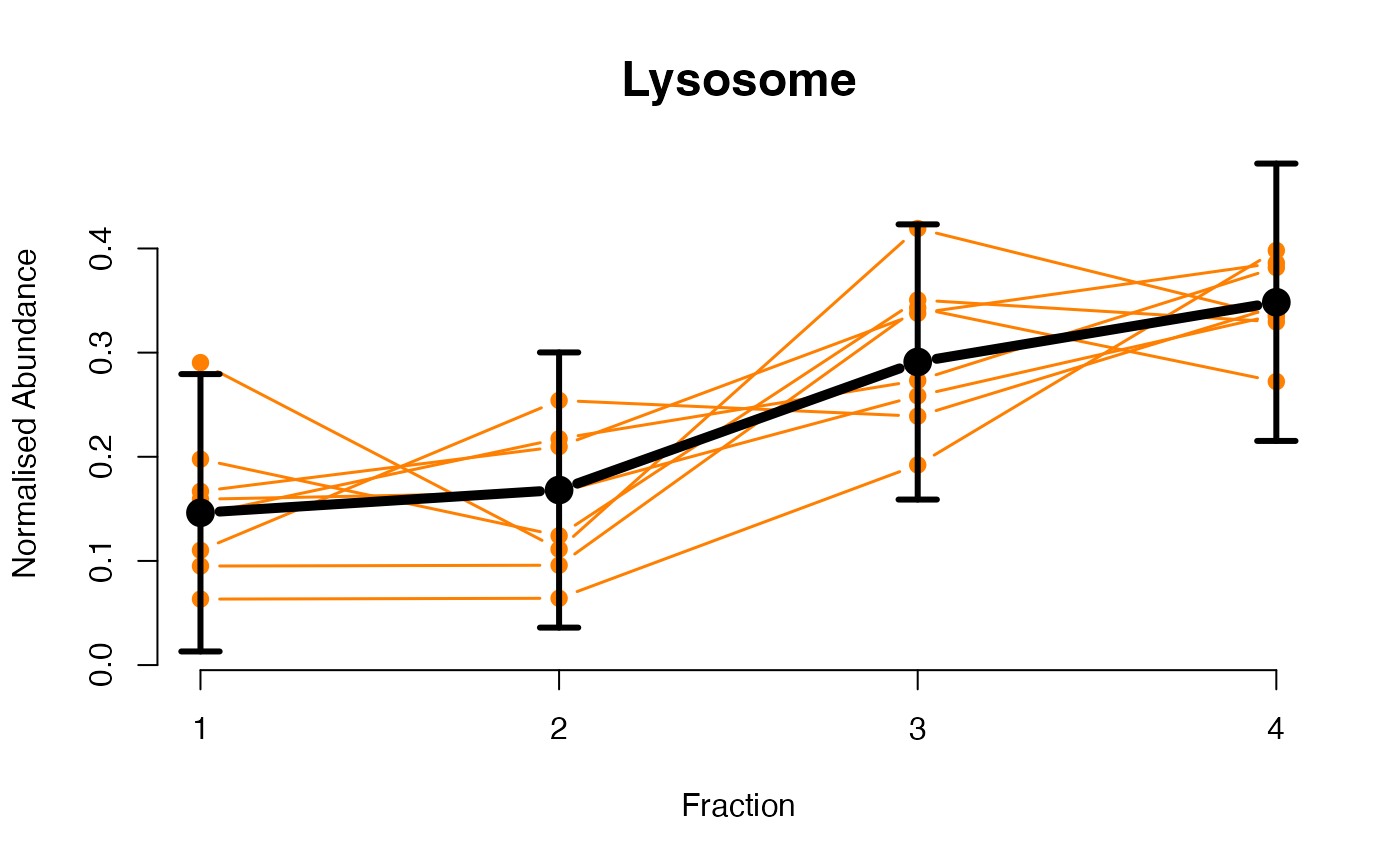
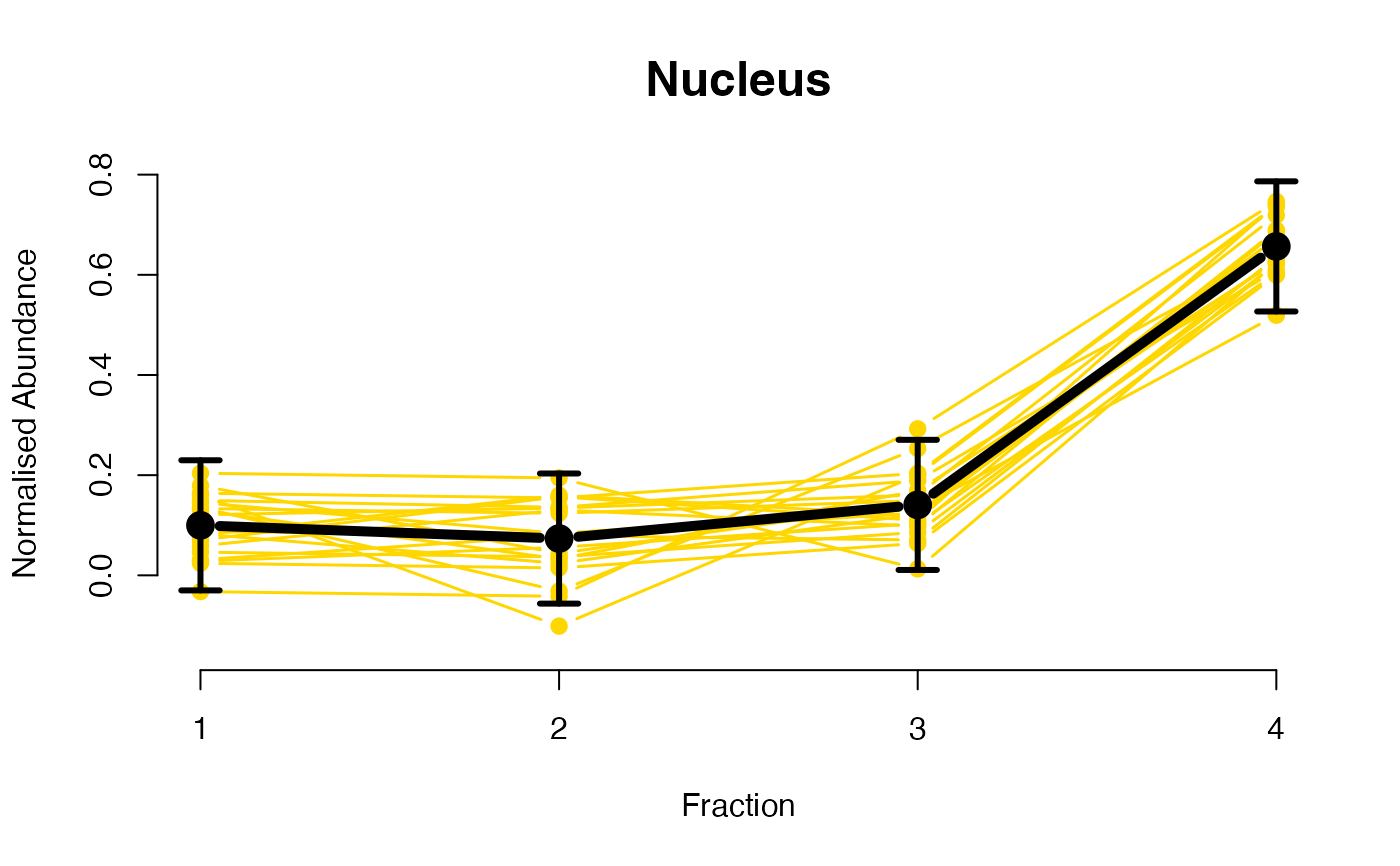

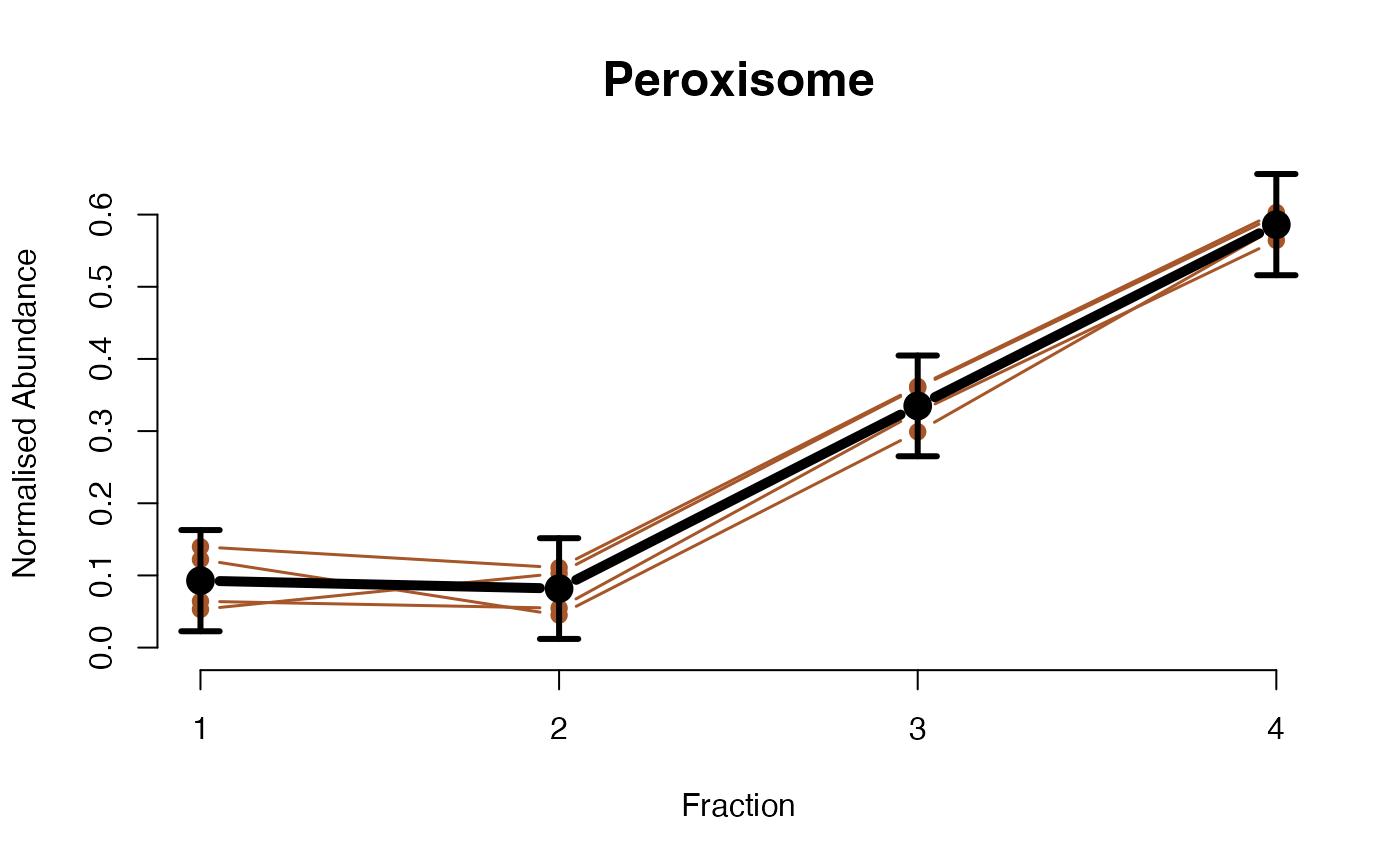

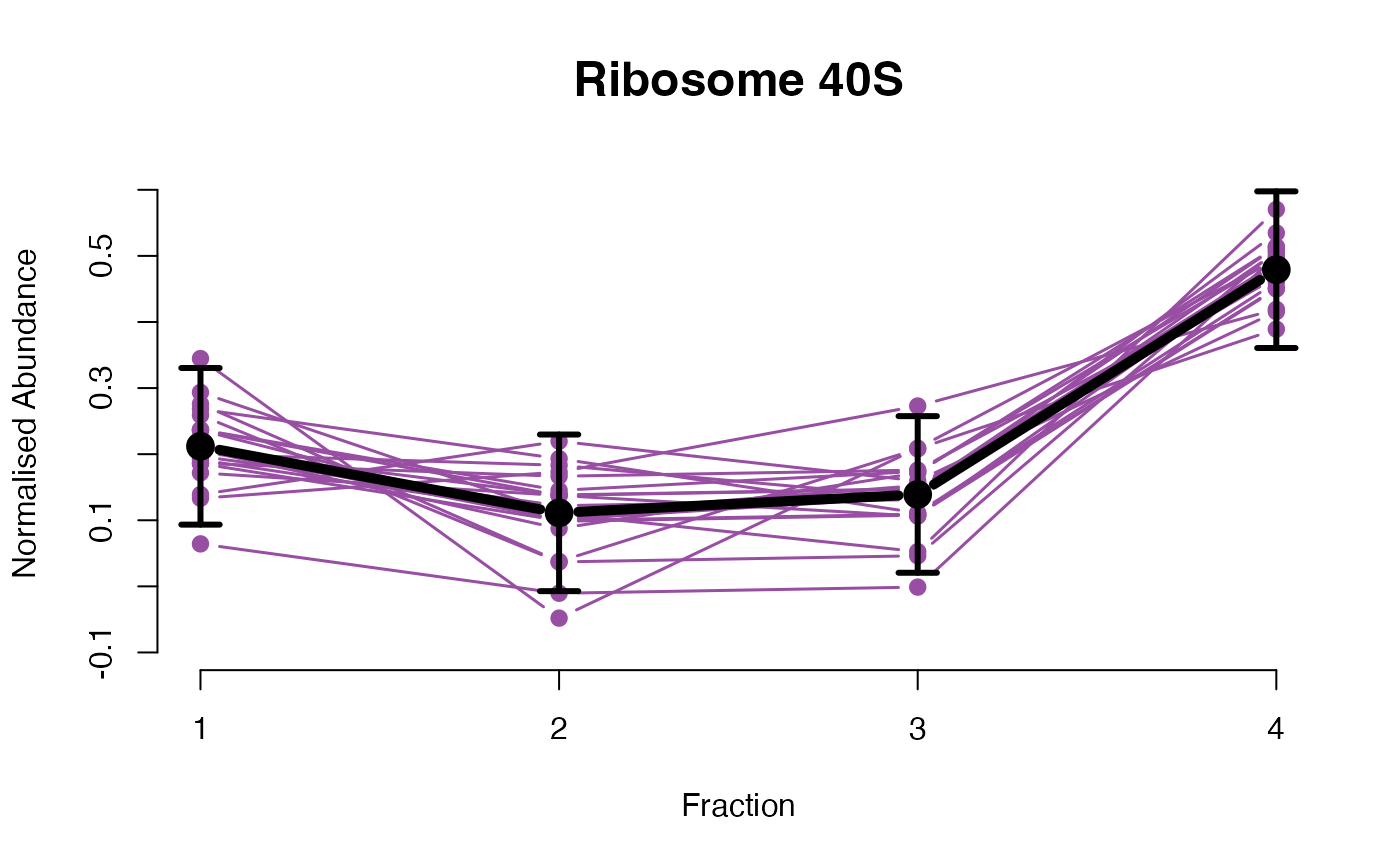



















 ## ====== fitGPmaternPC =====
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
## Please note that hyppar should be chosen carefully and tested
## by checking the GP fit with the plotGPmatern function
## (please see details above)
gpParams <- lapply(tansim$lopitrep,
function(x) fitGPmaternPC(x, hyppar = matrix(c(10, 60, 100), nrow = 1)))
## ====== fitGPmatern =====
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
gpParams <- lapply(tansim$lopitrep, function(x) fitGPmaternPC(x))
## ====== plotGPmatern =====
## generate example data
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
## fit a GP
gpParams <- lapply(tansim$lopitrep, function(x) fitGP(x))
## ====== fitGPmaternPC =====
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
## Please note that hyppar should be chosen carefully and tested
## by checking the GP fit with the plotGPmatern function
## (please see details above)
gpParams <- lapply(tansim$lopitrep,
function(x) fitGPmaternPC(x, hyppar = matrix(c(10, 60, 100), nrow = 1)))
## ====== fitGPmatern =====
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
gpParams <- lapply(tansim$lopitrep, function(x) fitGPmaternPC(x))
## ====== plotGPmatern =====
## generate example data
library(pRolocdata)
data("tan2009r1")
set.seed(1)
tansim <- sim_dynamic(object = tan2009r1,
numRep = 6L,
numDyn = 100L)
## fit a GP
gpParams <- lapply(tansim$lopitrep, function(x) fitGP(x))
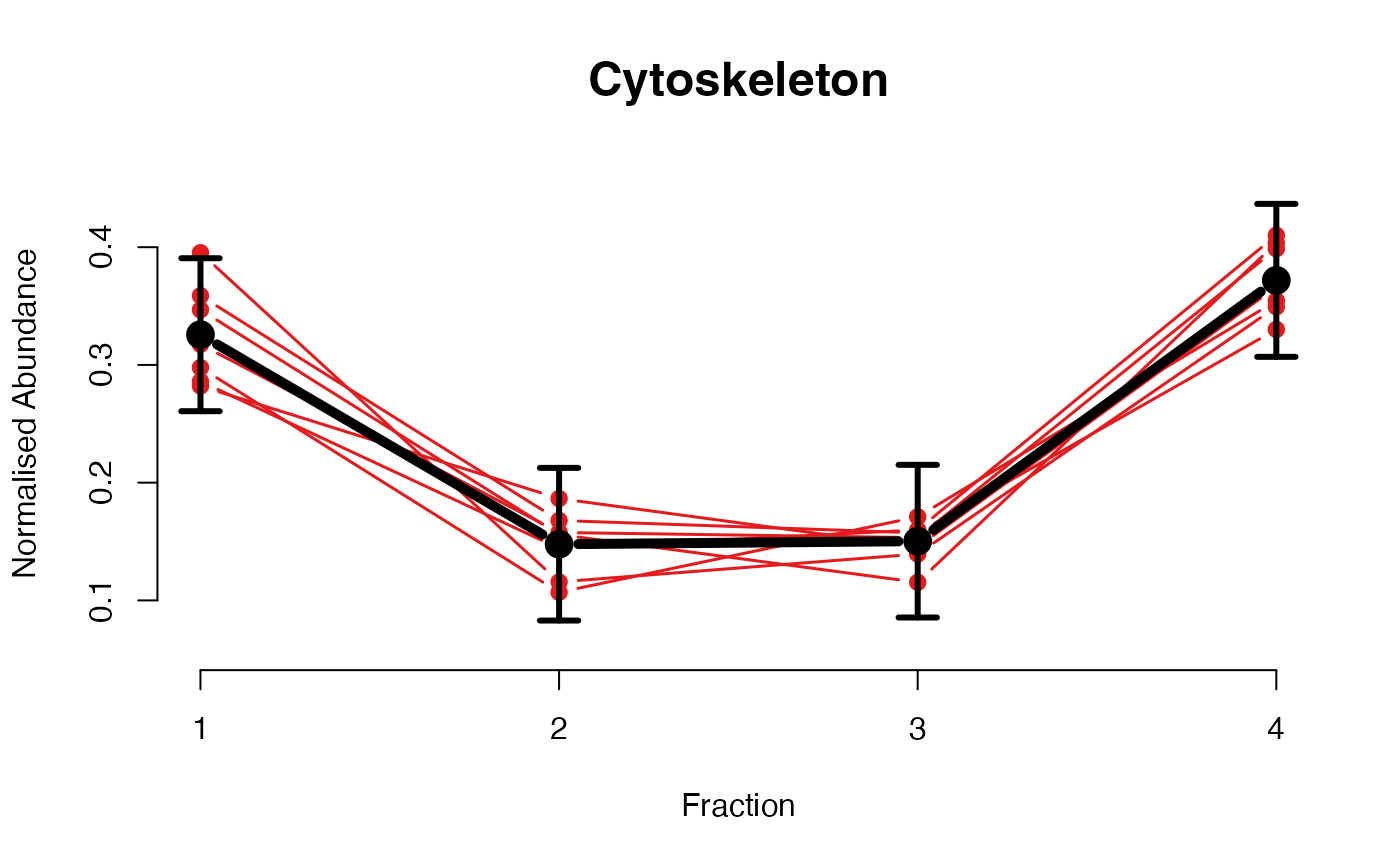

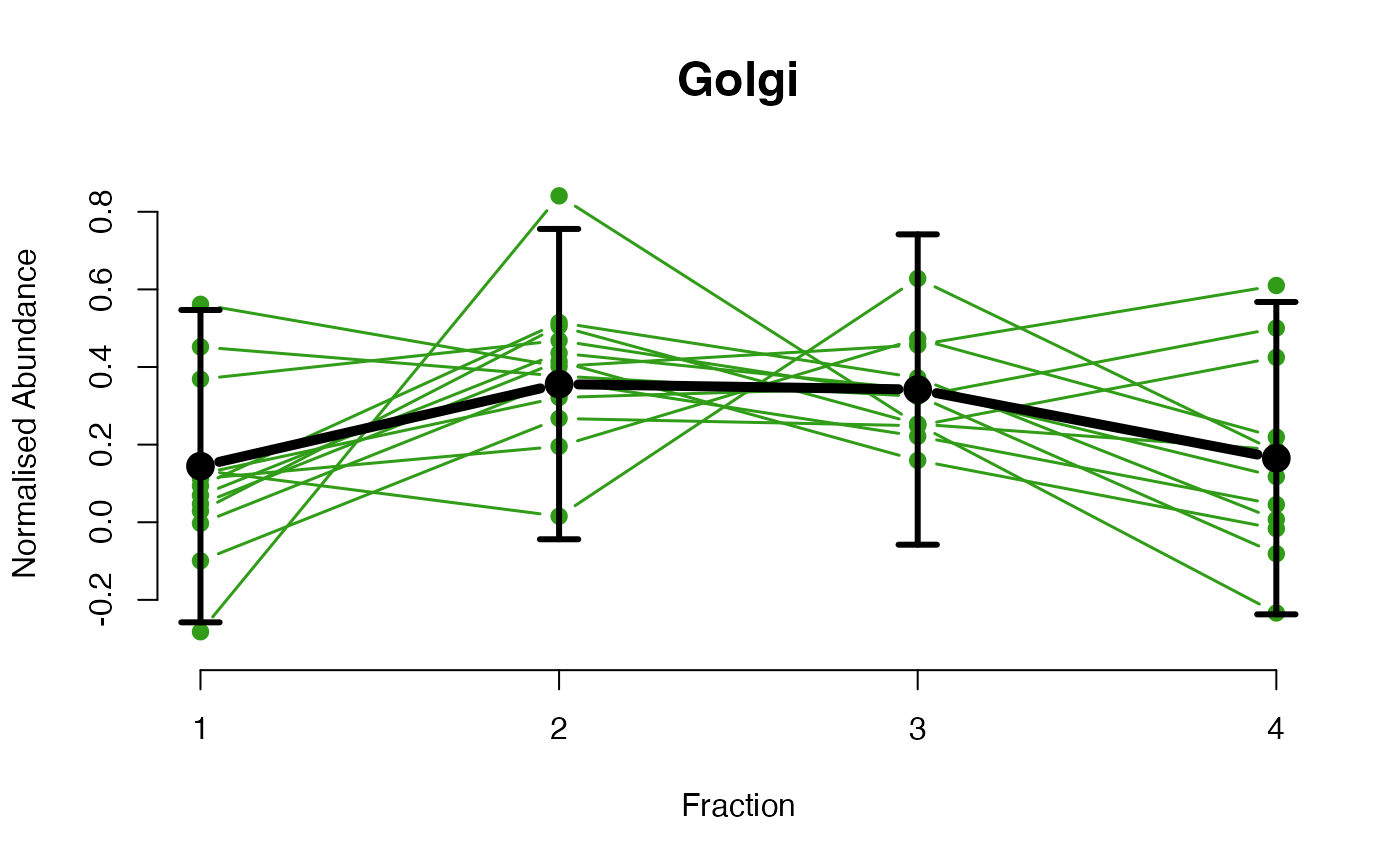
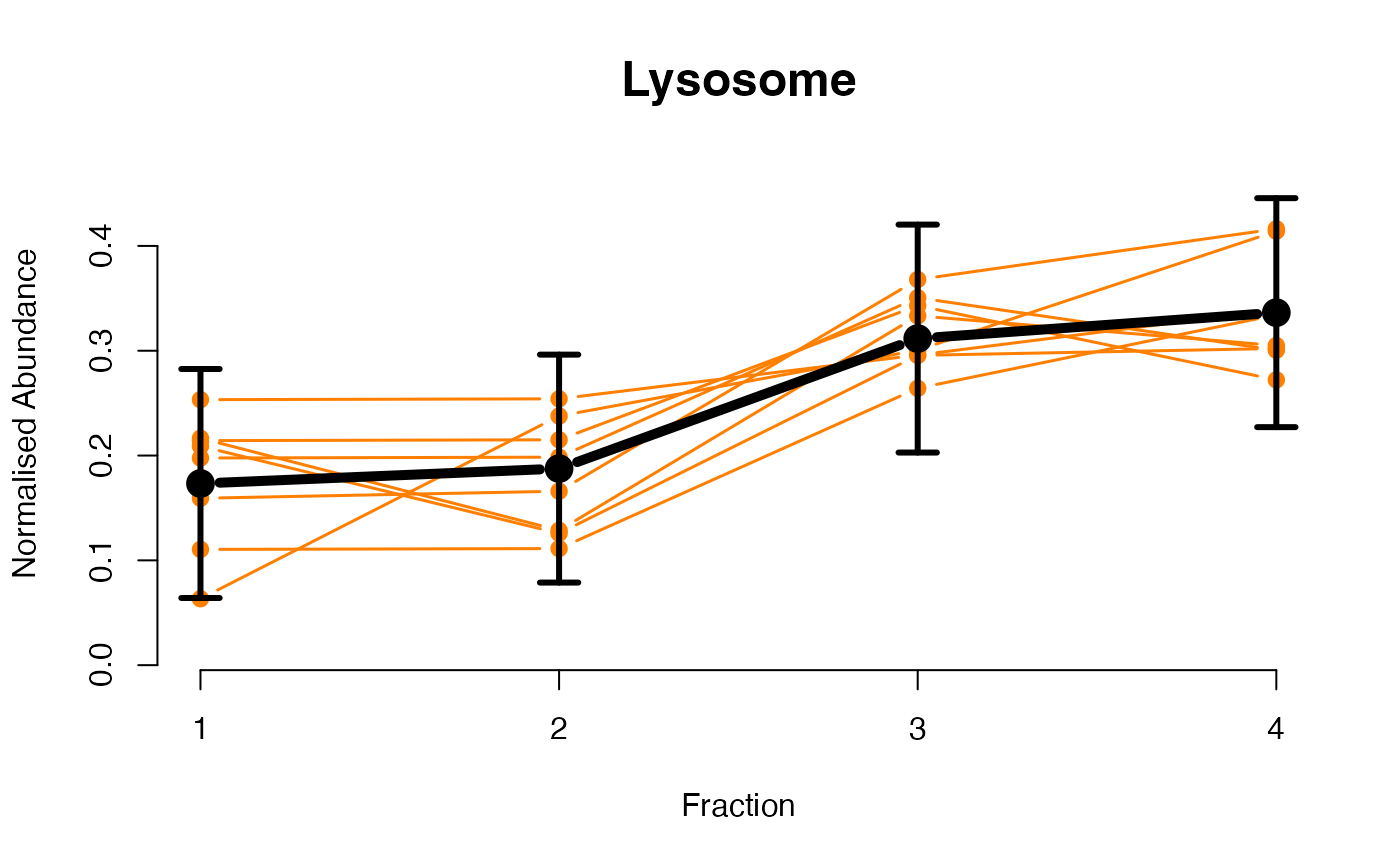

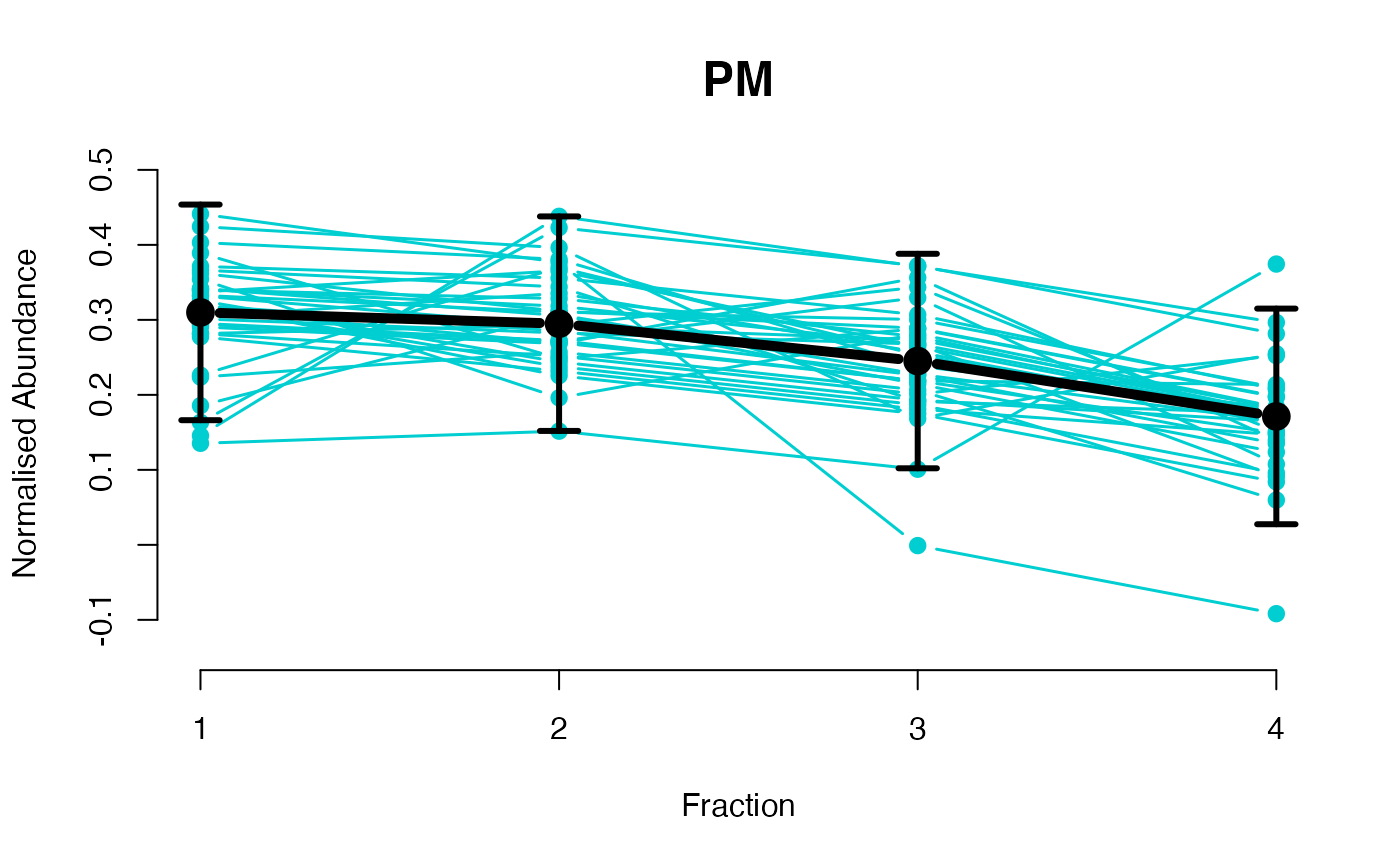

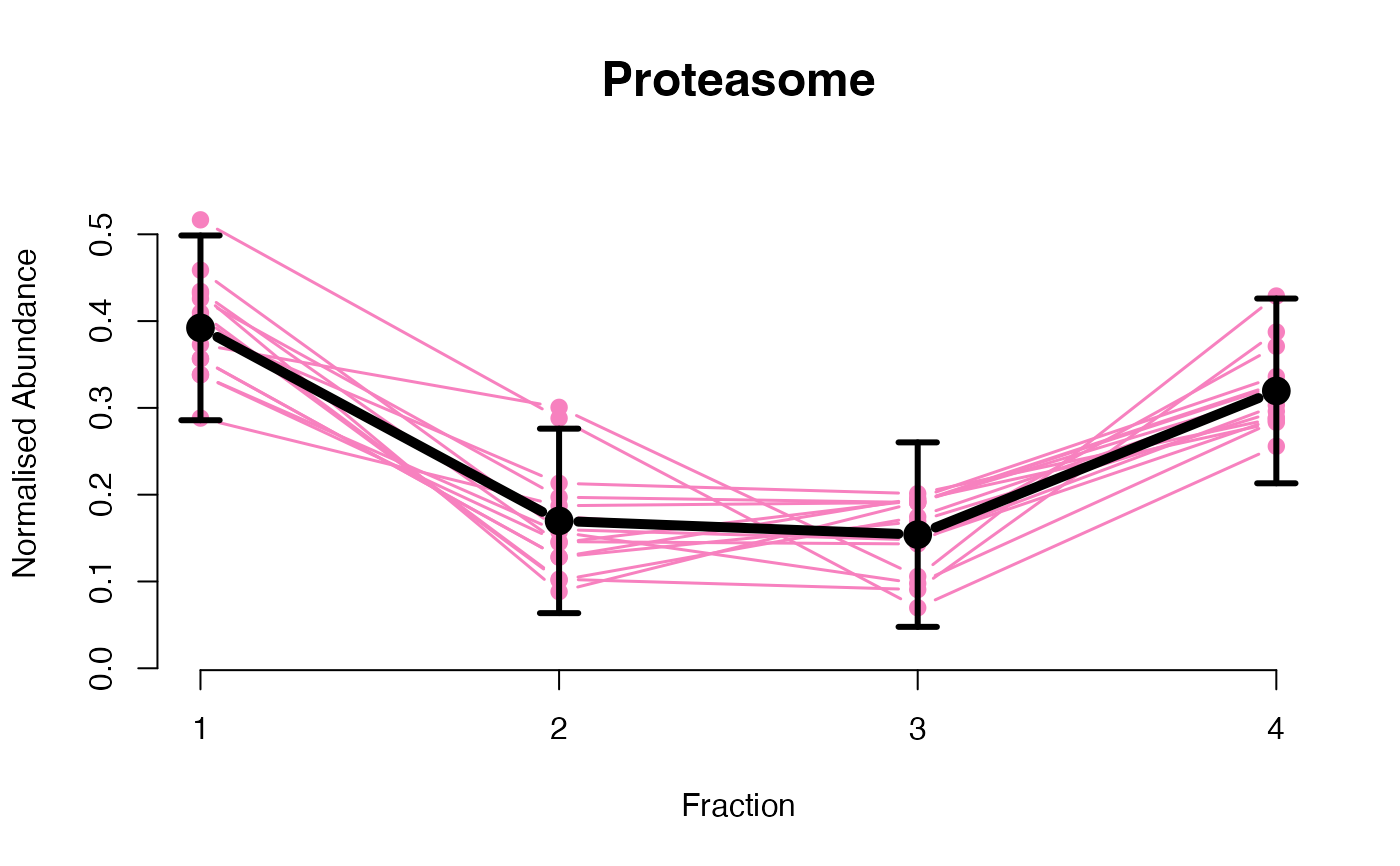
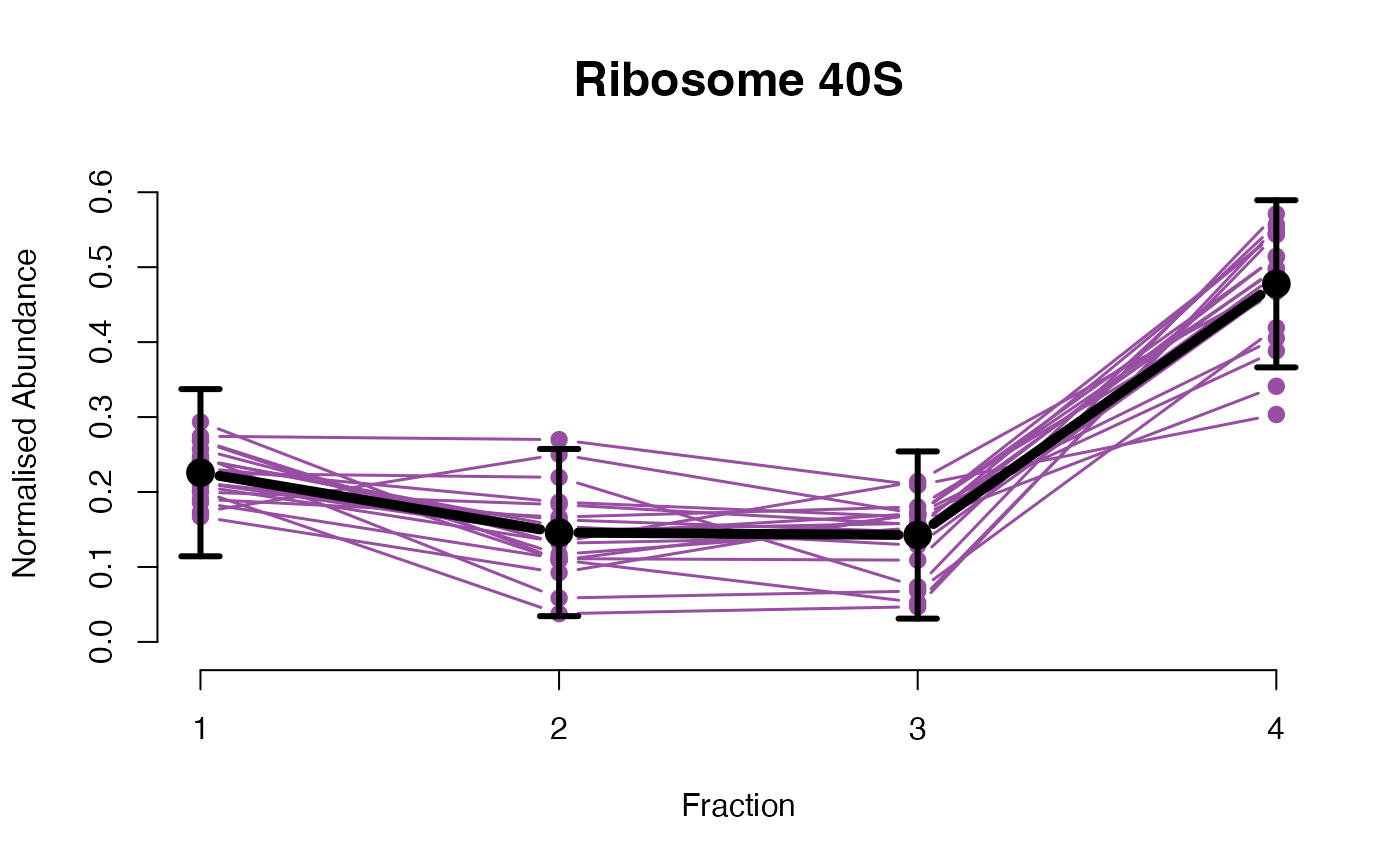
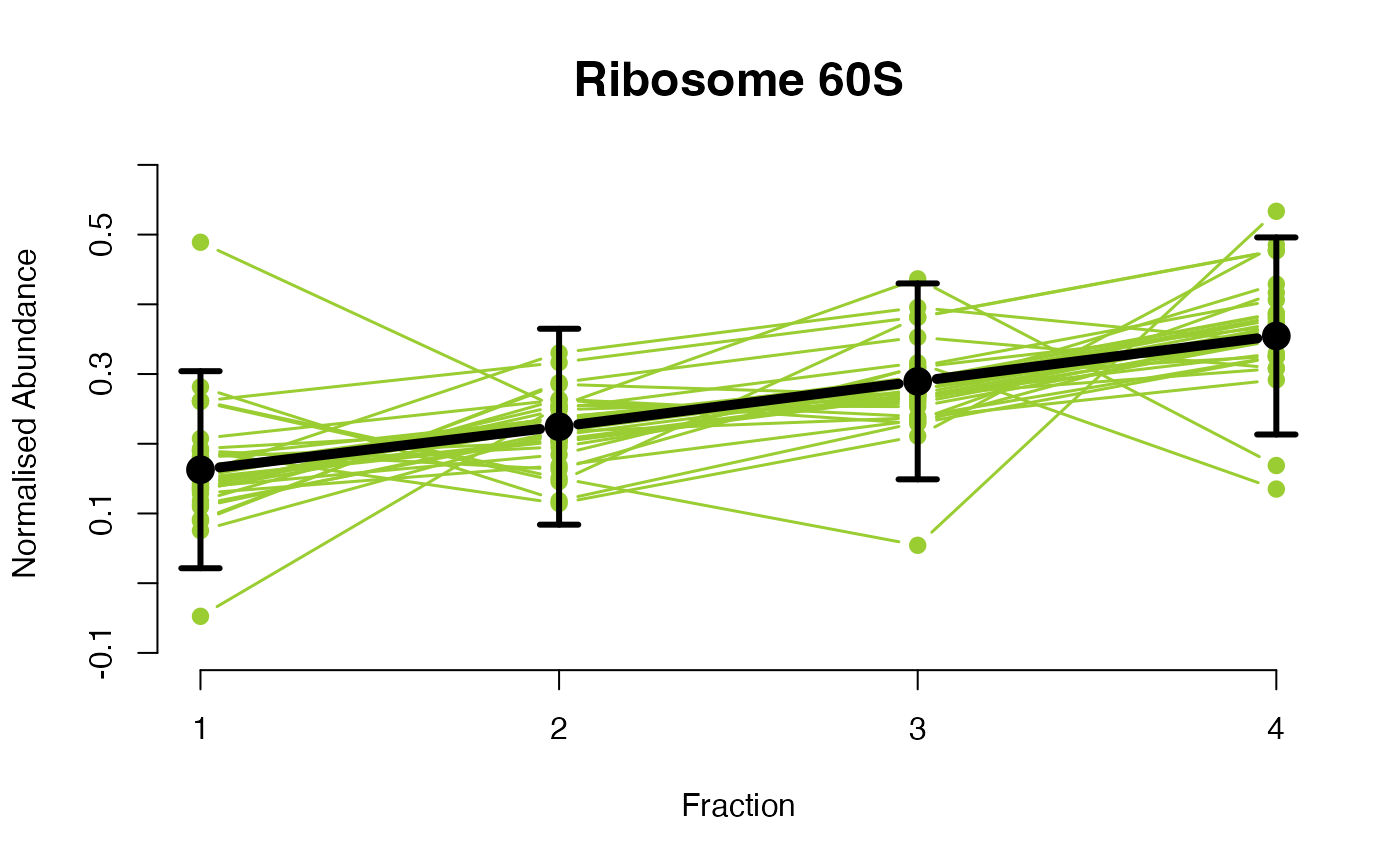

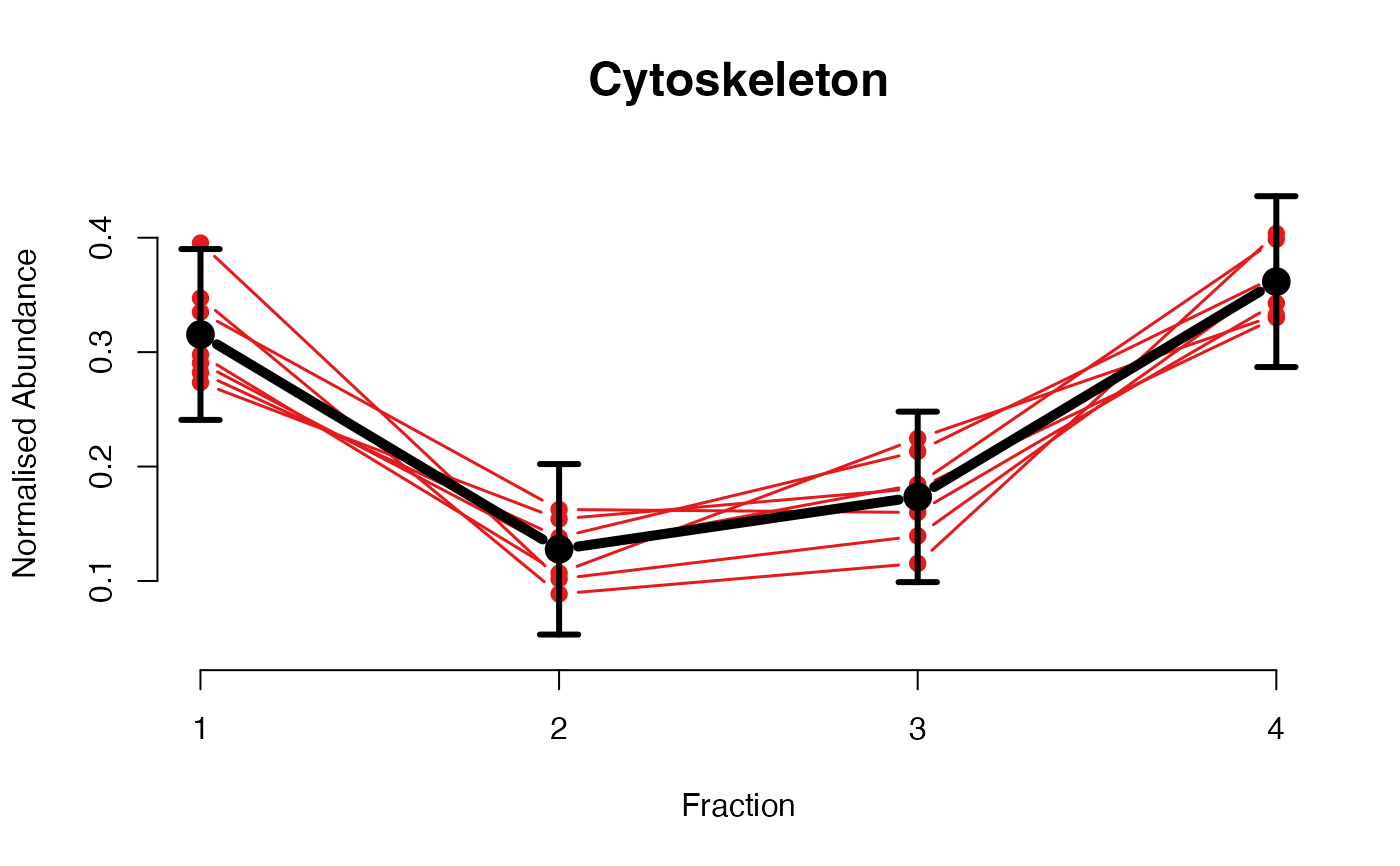
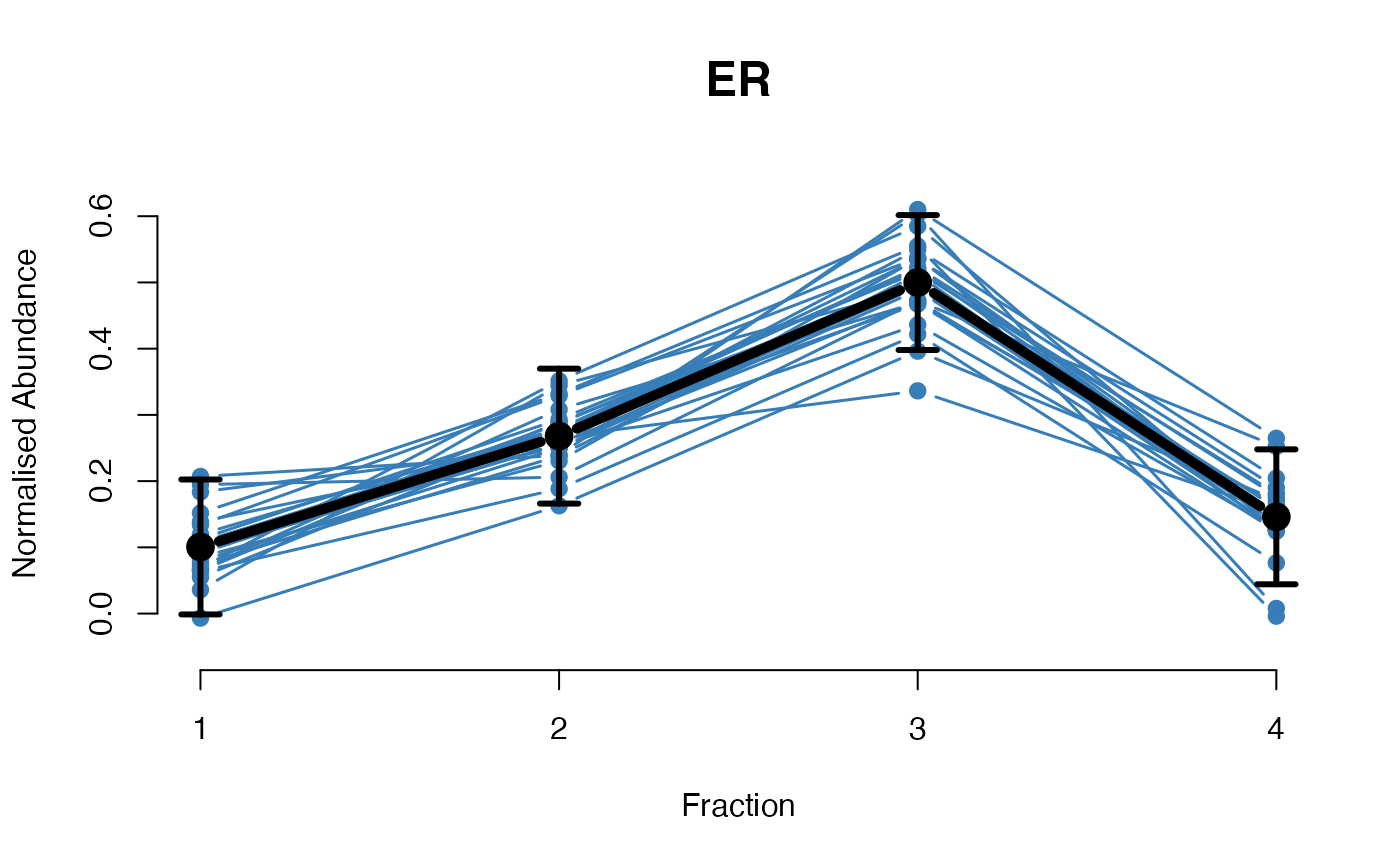
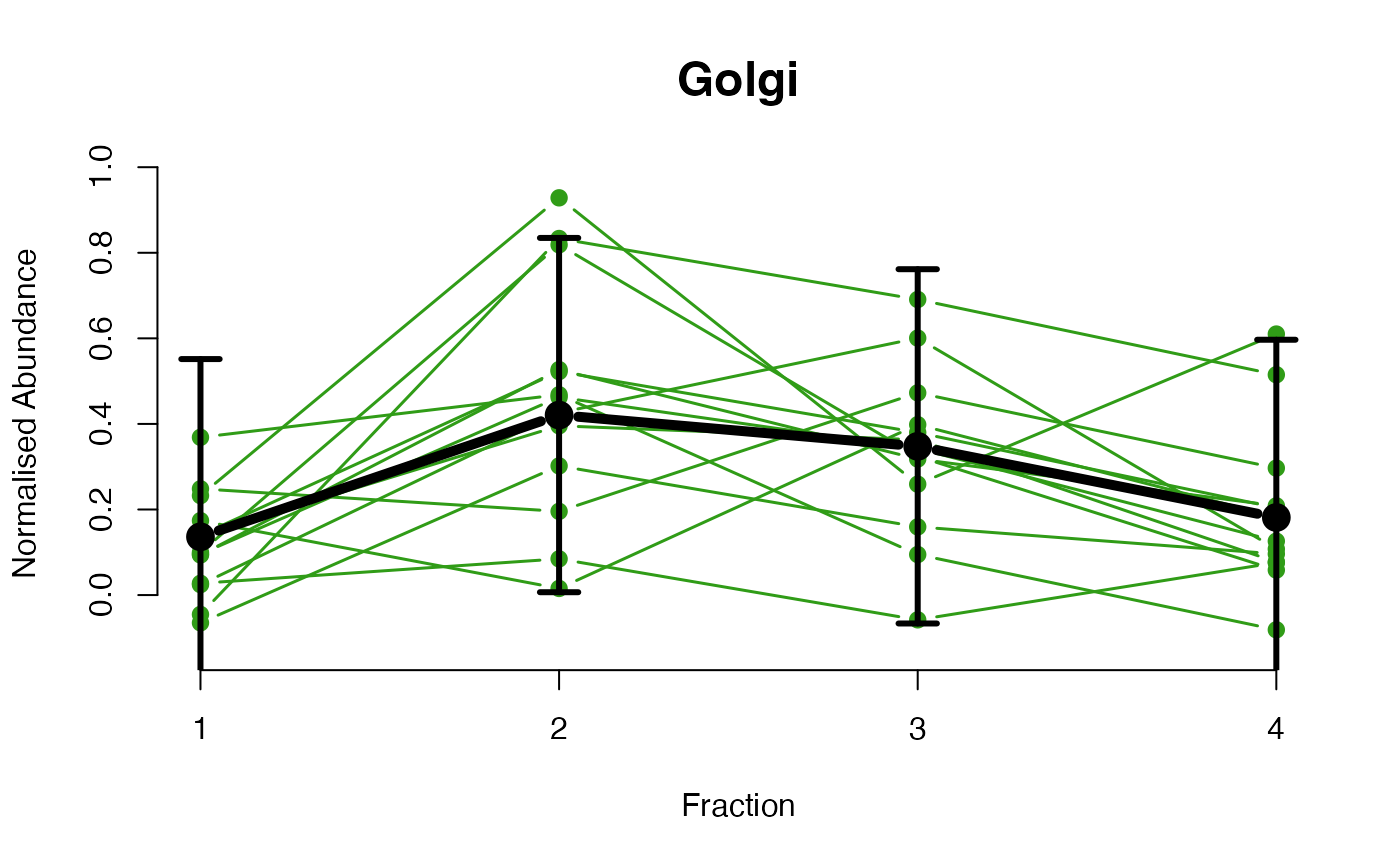



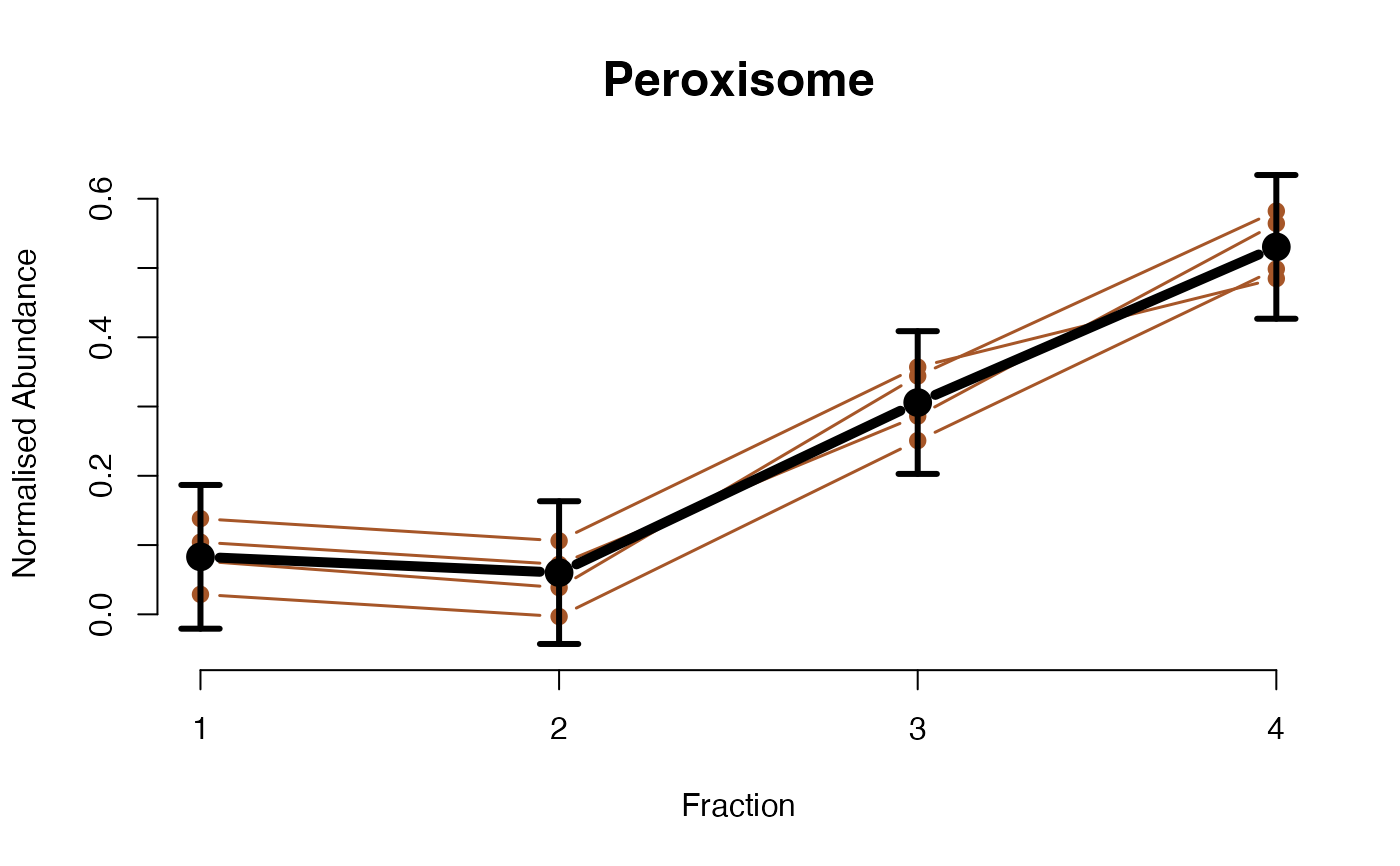




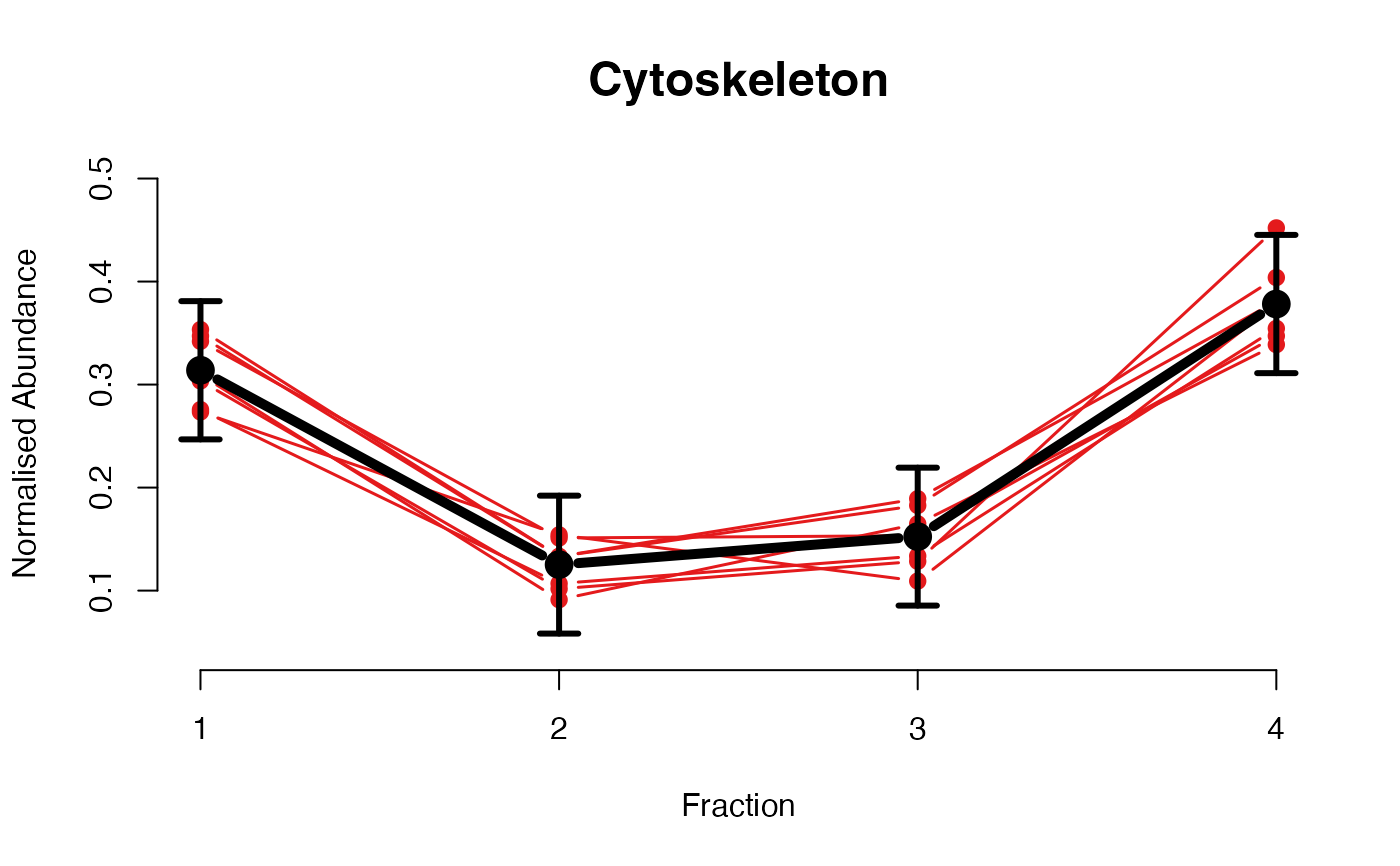
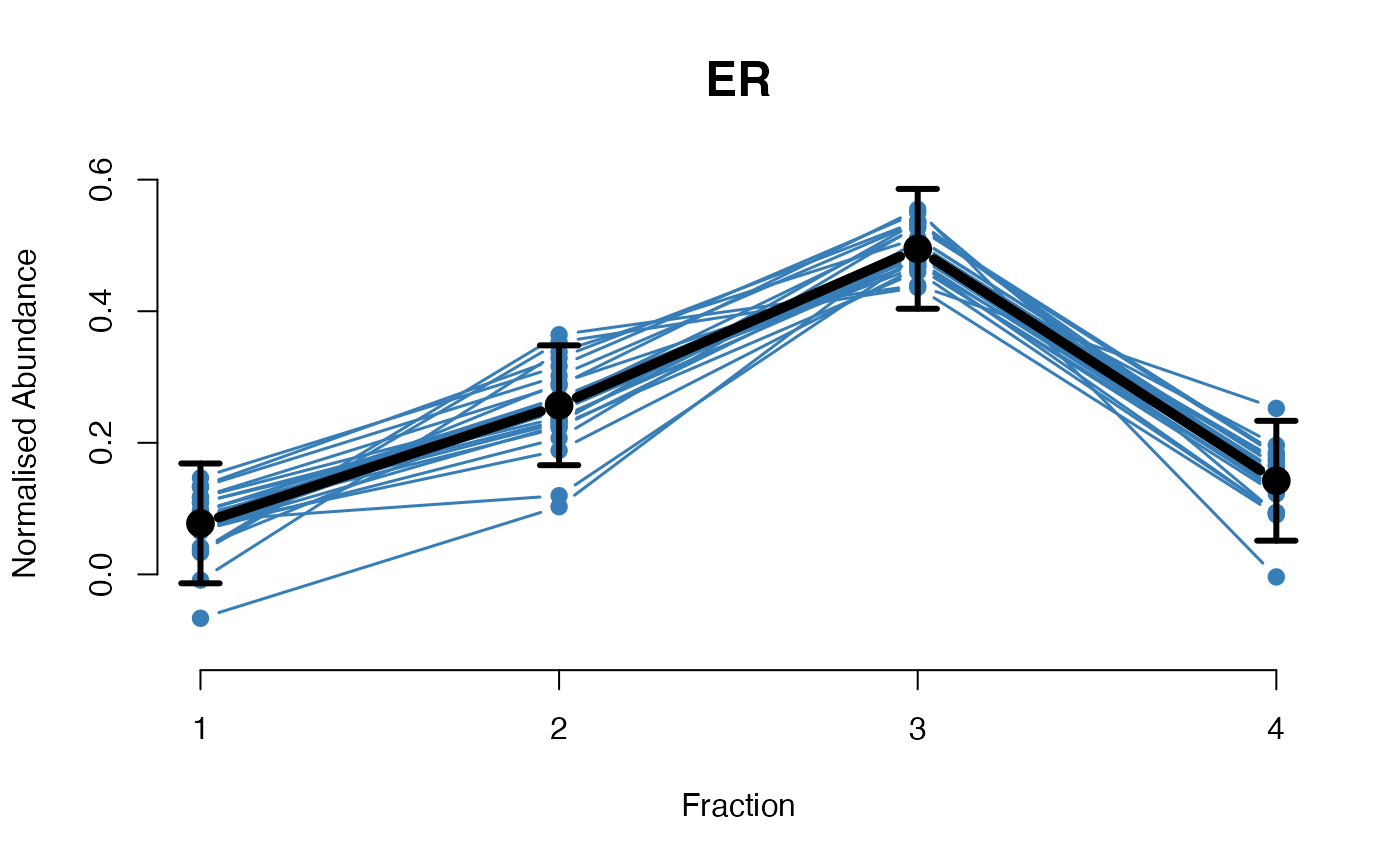






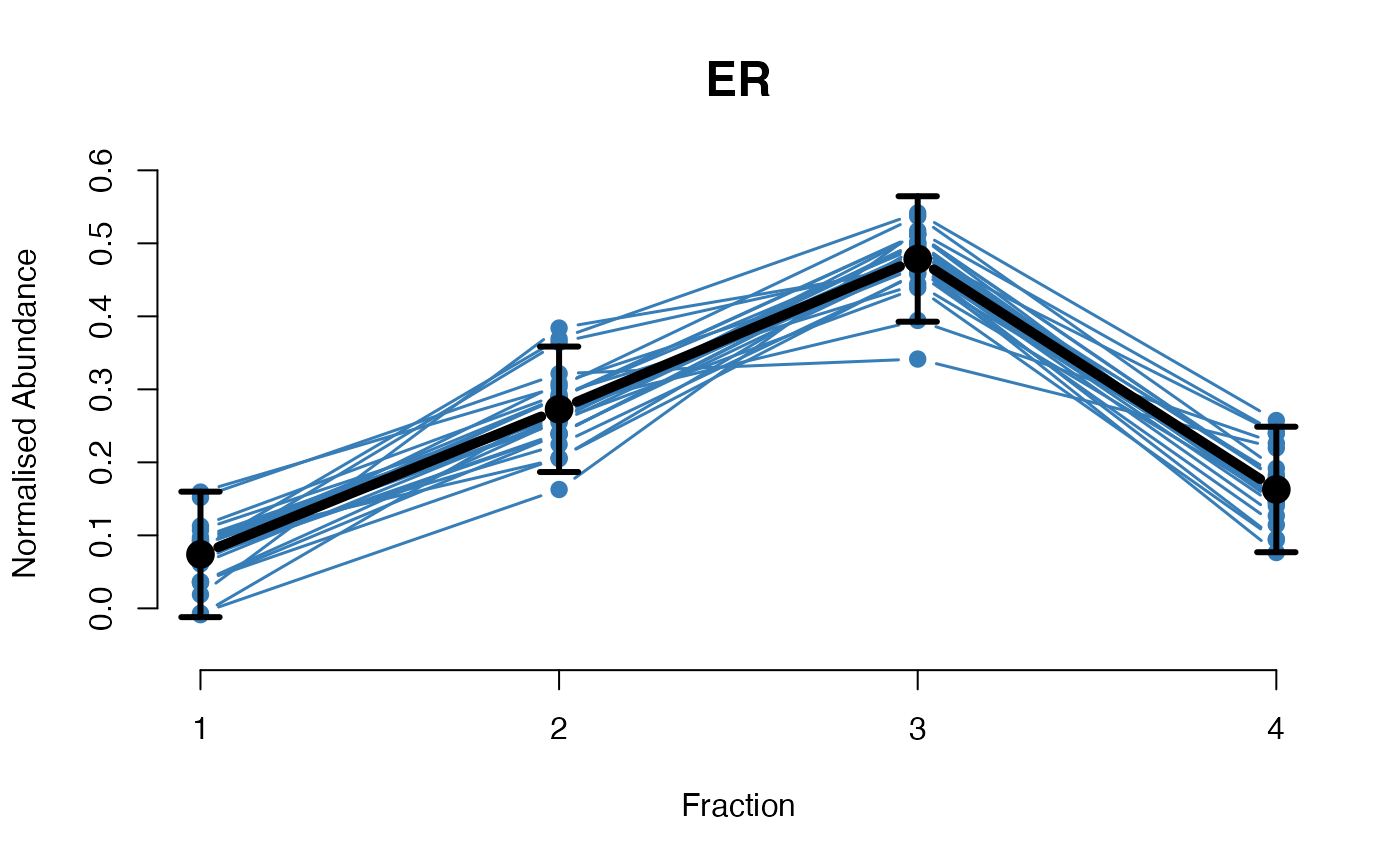

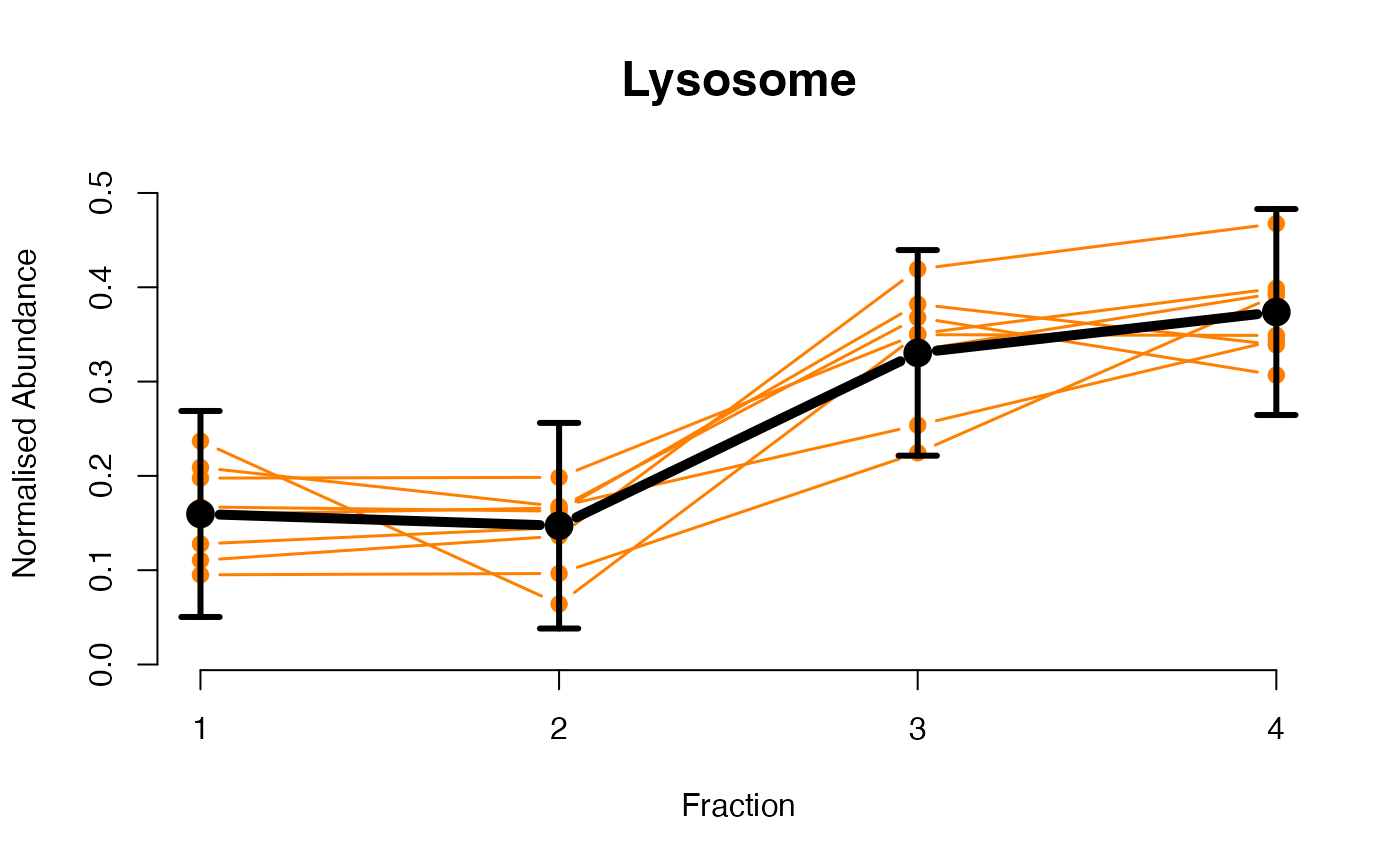

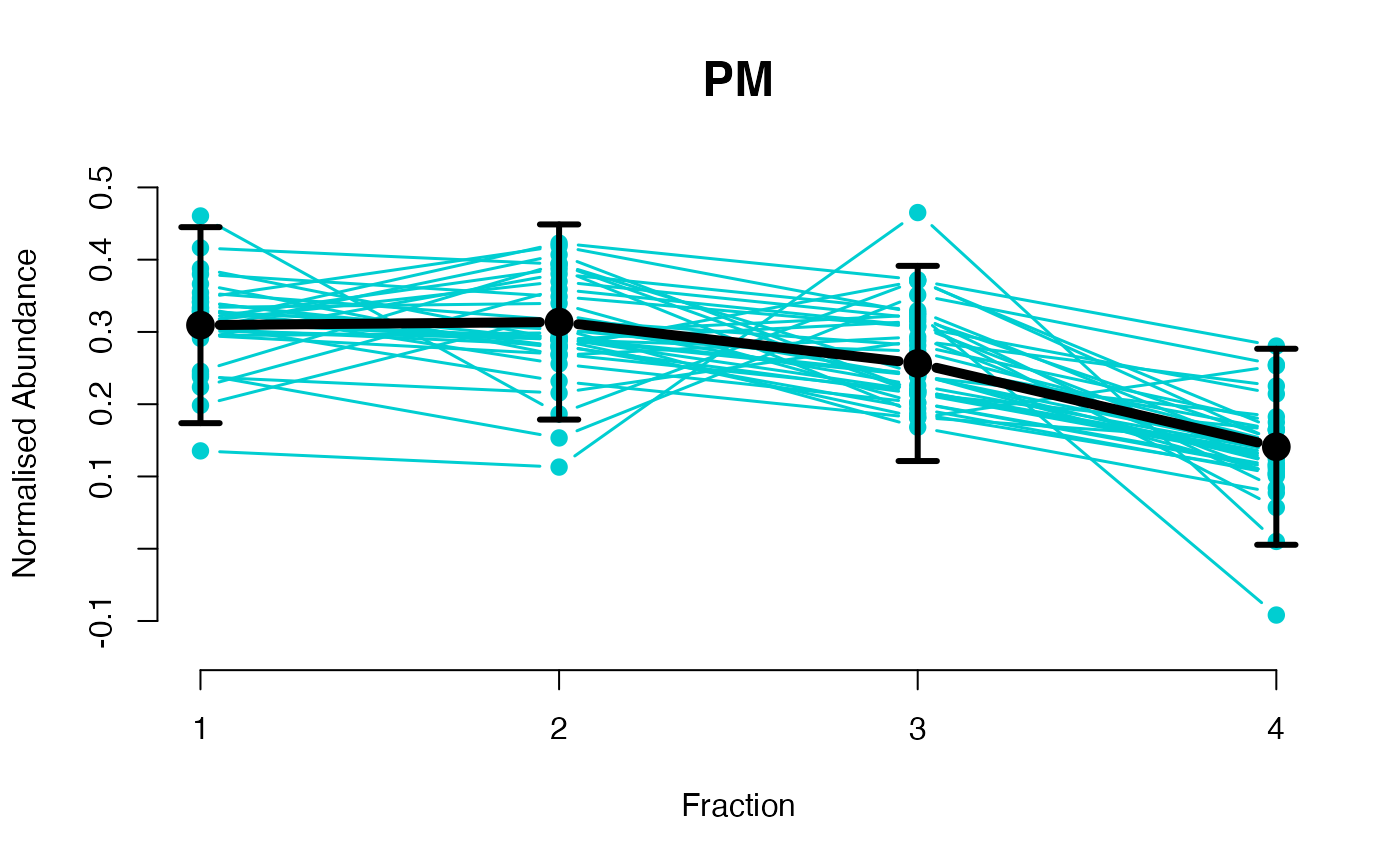
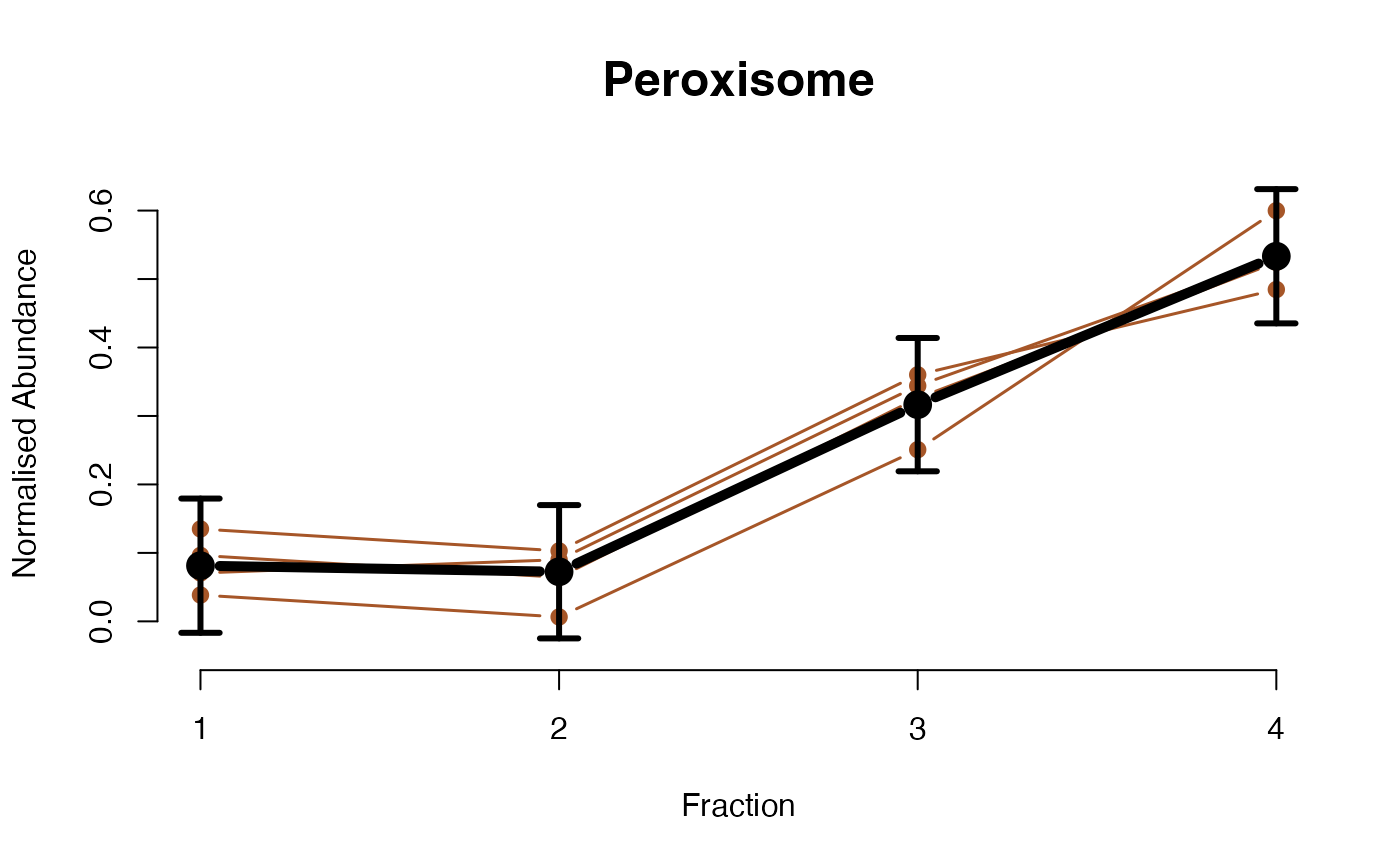





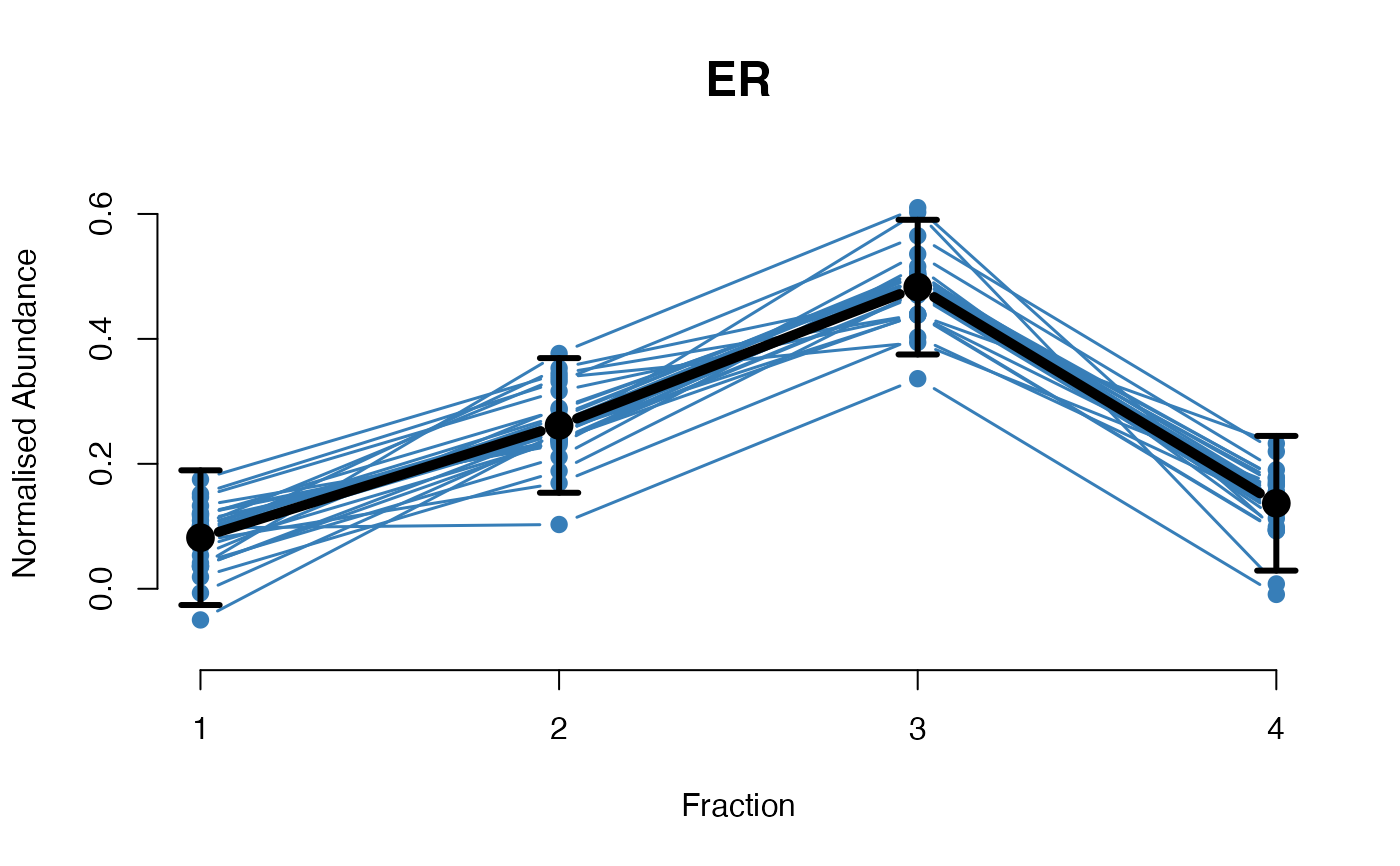


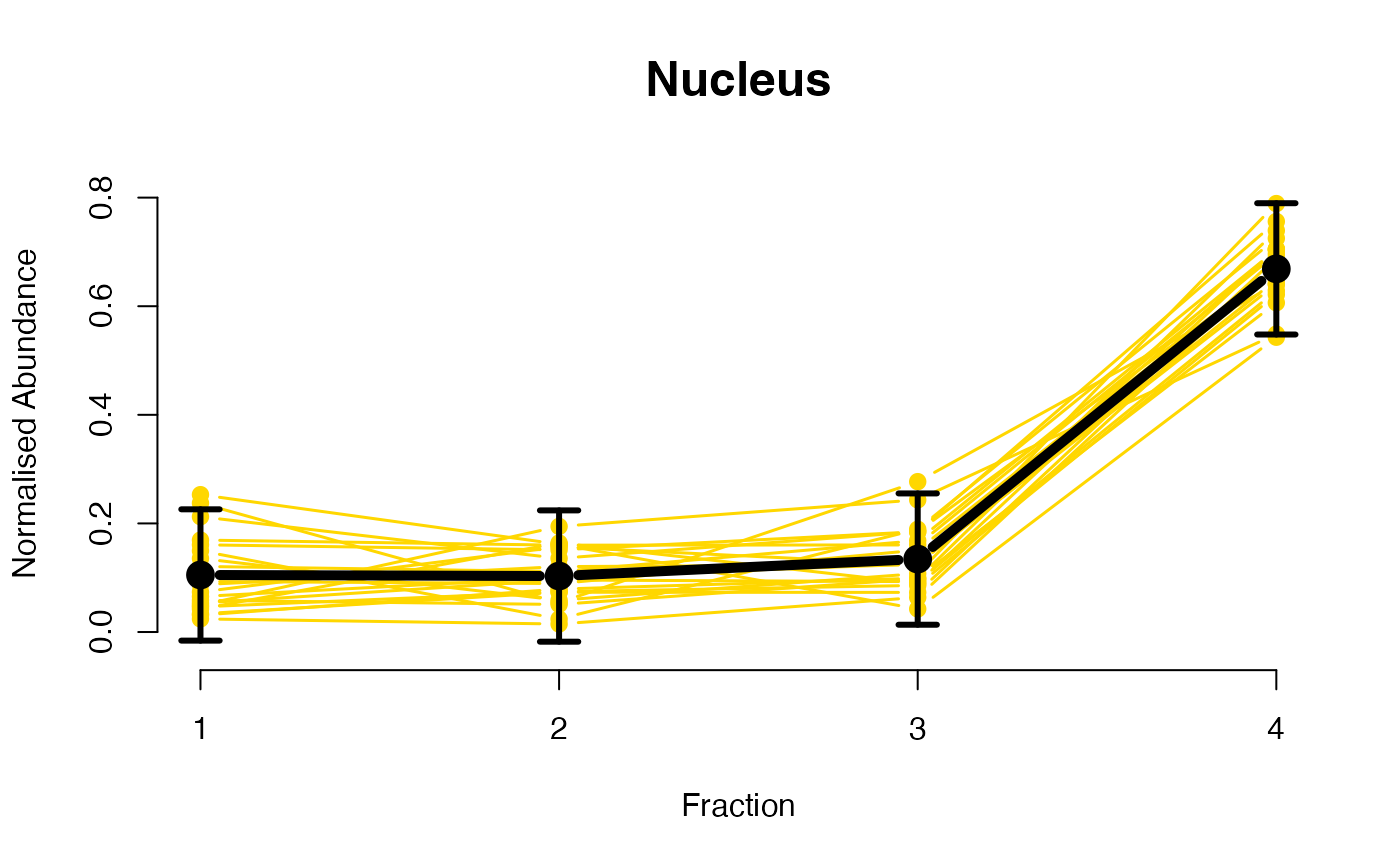
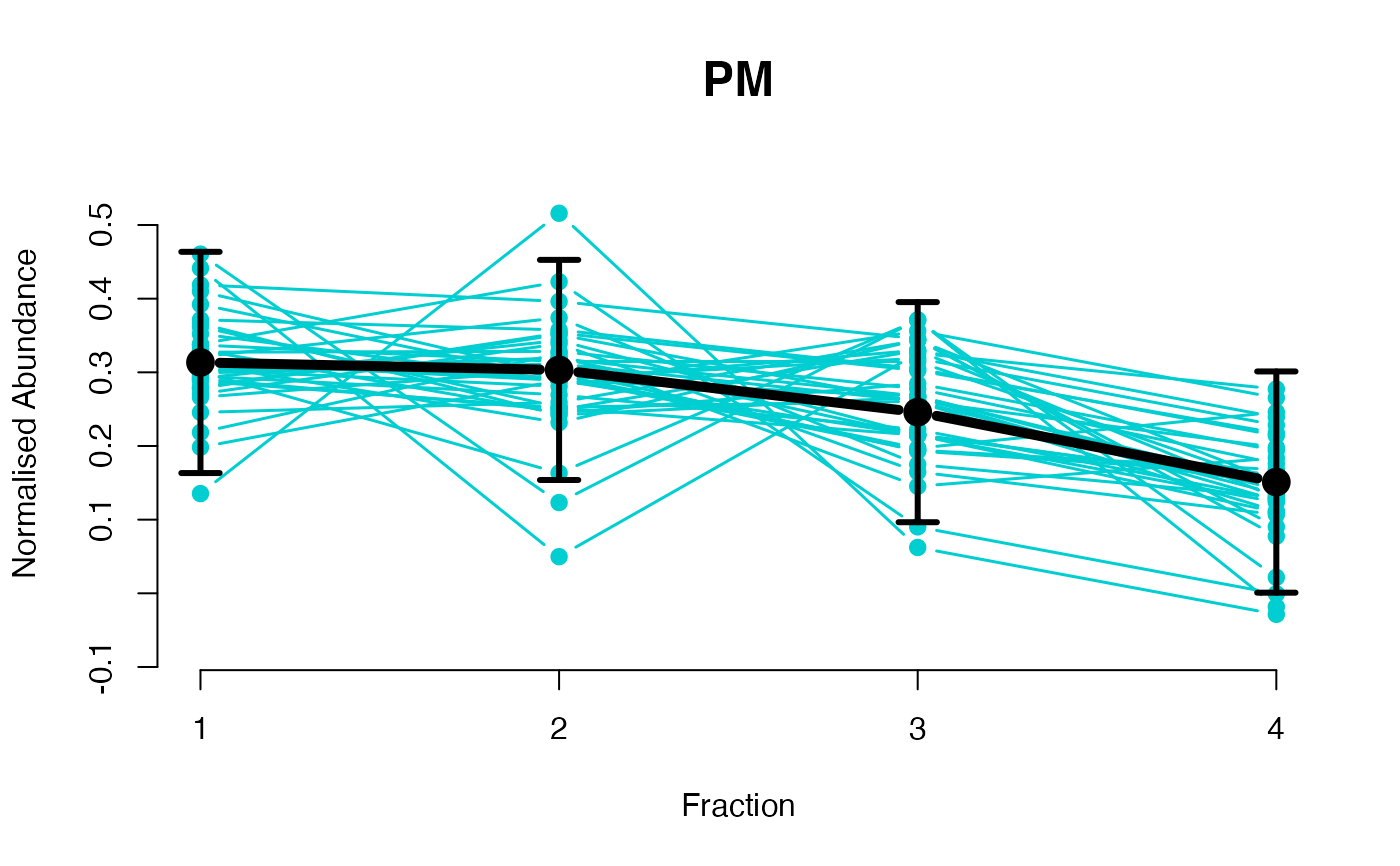


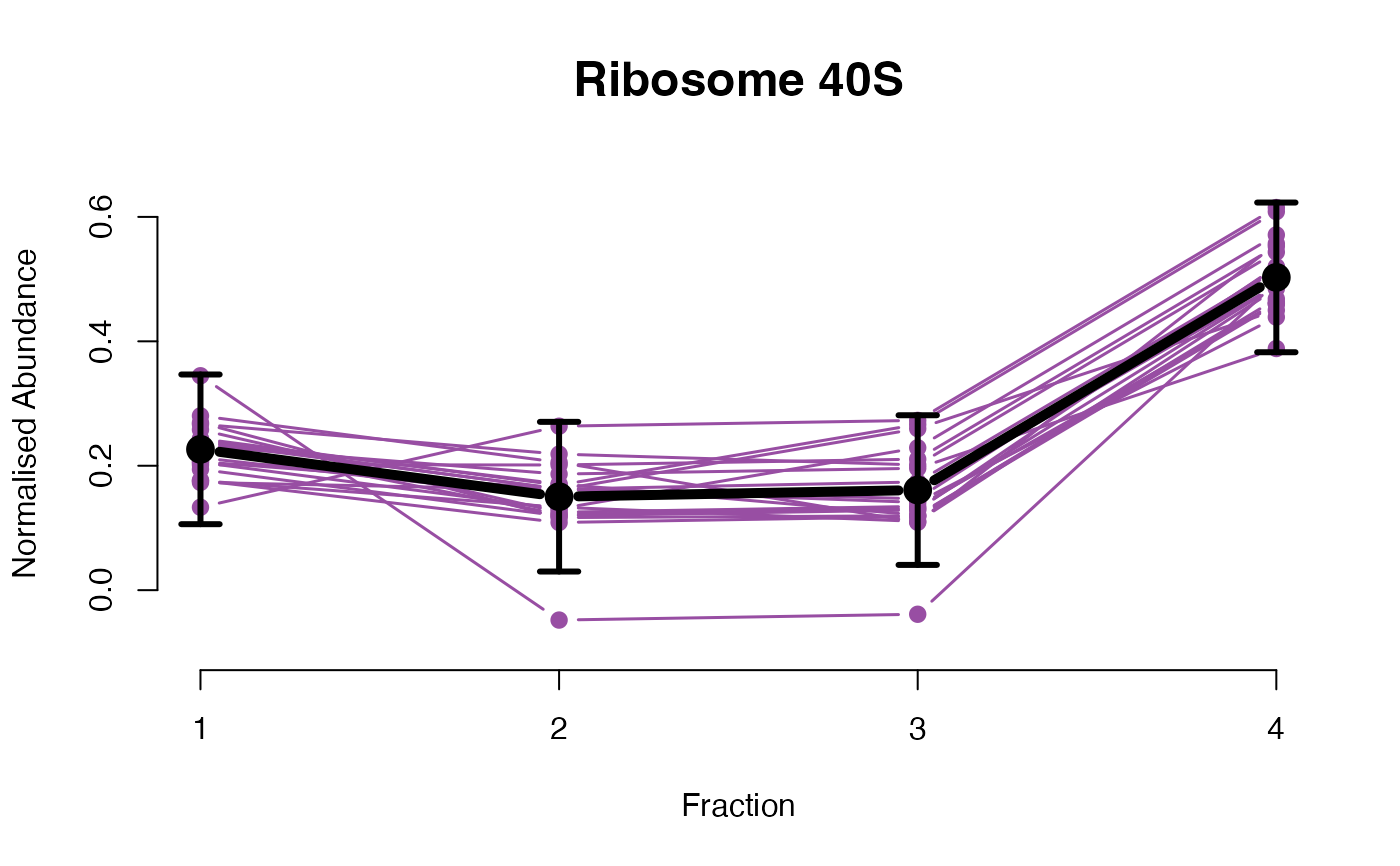

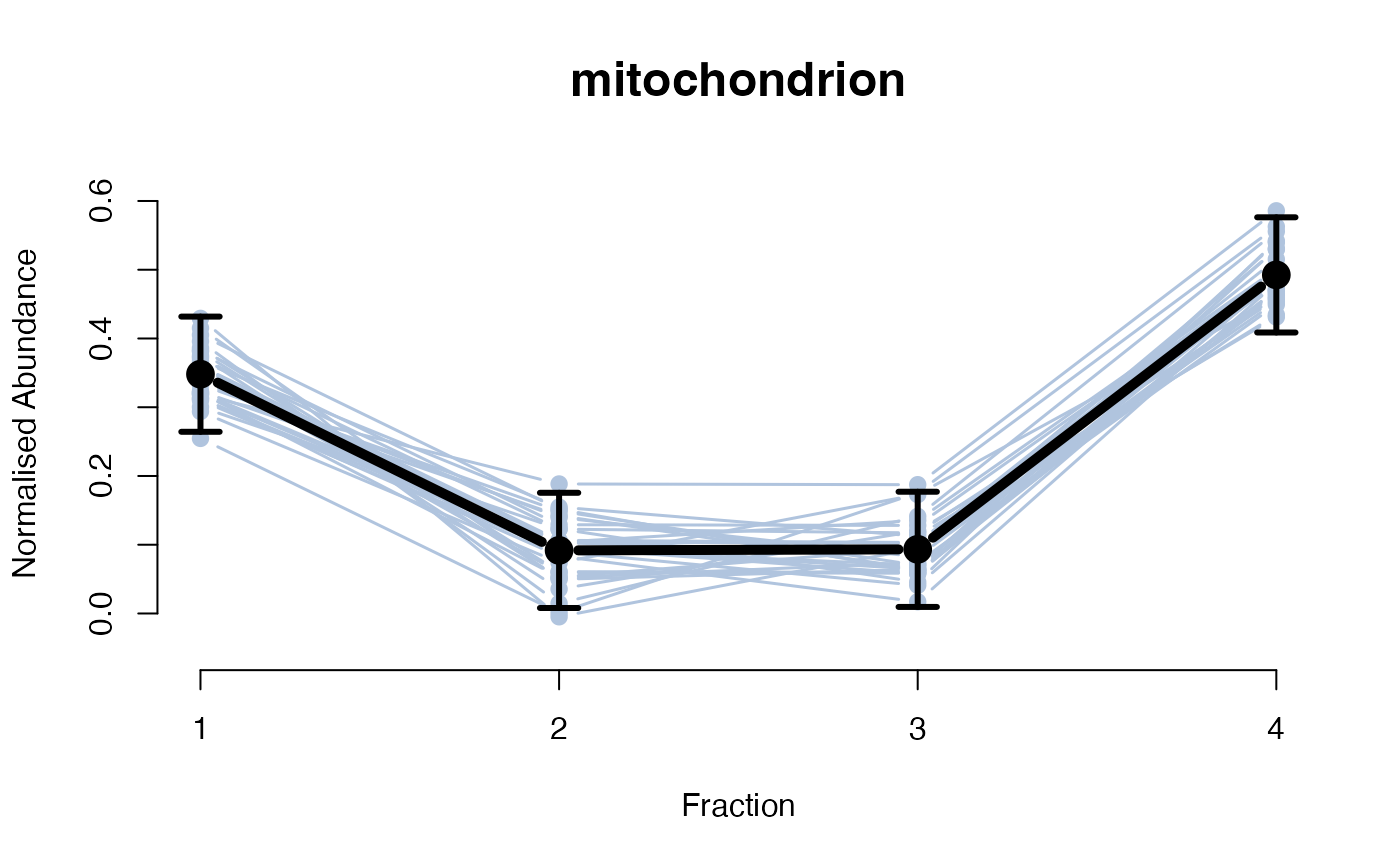
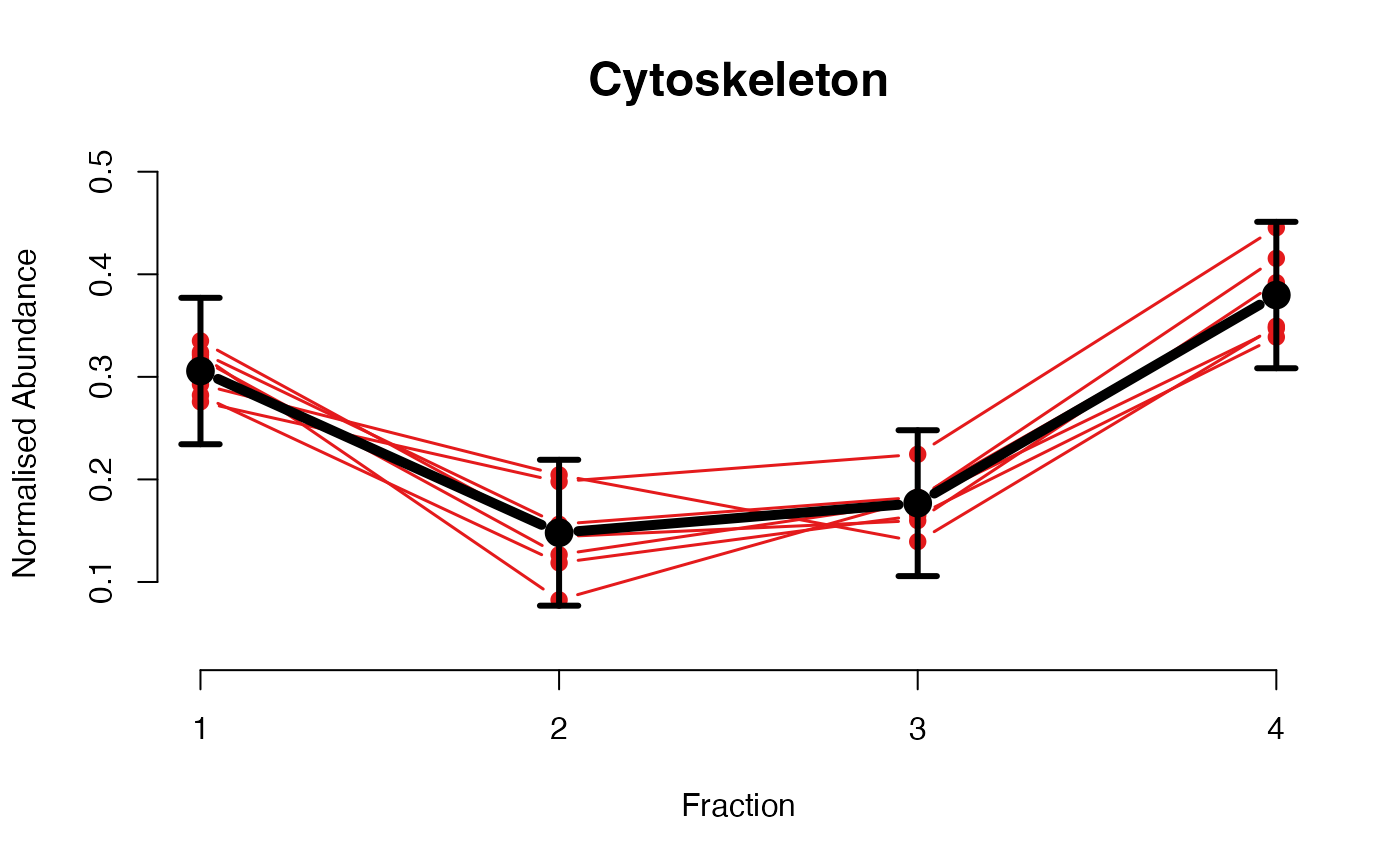
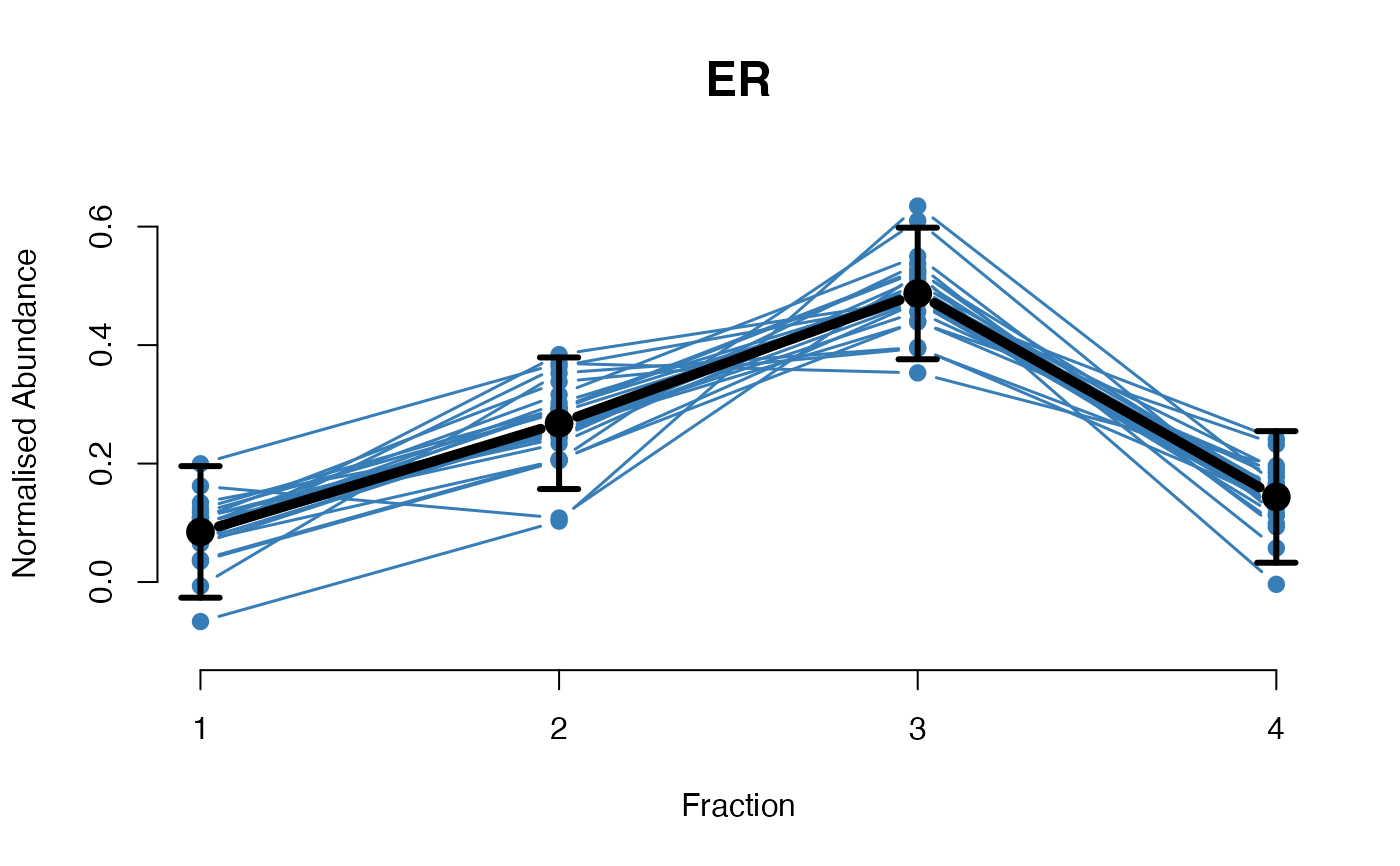

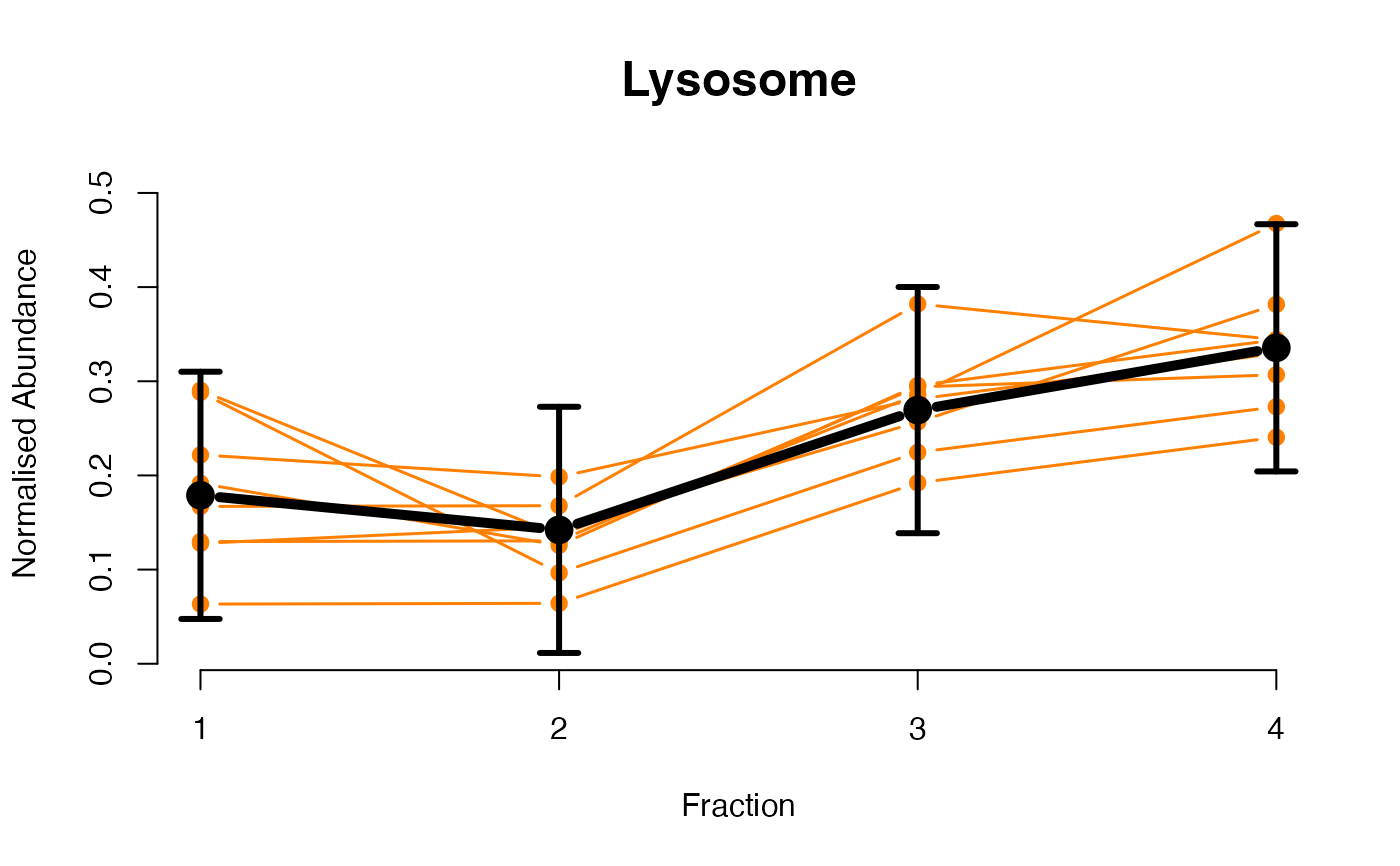



 ## Overlay posterior predictives onto profiles
## Dataset1 1
par(mfrow = c(2, 3))
plotGPmatern(tansim$lopitrep[[1]], gpParams[[1]])
## Overlay posterior predictives onto profiles
## Dataset1 1
par(mfrow = c(2, 3))
plotGPmatern(tansim$lopitrep[[1]], gpParams[[1]])
 ## Dataset 2, etc.
par(mfrow = c(2, 3))
## Dataset 2, etc.
par(mfrow = c(2, 3))
 plotGPmatern(tansim$lopitrep[[2]], gpParams[[2]])
plotGPmatern(tansim$lopitrep[[2]], gpParams[[2]])

